微结构波导管的谐振特性研究

利用THz-TDS系统测量了光栅朝向为0°和90°的时域信号,作为对比,还测量了THz波通过空气及透过空白波导管时的参考信号,如图6.11(a)所示。经过波导管的时域信号均可以分为两个脉冲周期,第一个脉冲周期与空气参考信号相比没有时间延迟,因此可看作是从波导管空气孔直接透射的THz信号,光栅结构对其不产生影响;第二个脉冲周期与第一个脉冲周期相比有一个3.84 ps的时间延迟,这是由于THz波与管壁相互作用并形成谐振,如图6.10(c)所示,从而导致了时间延迟及色散的发生。另外,由于波导管外表面存在的周期性结构改变了管壁的相对折射率,从而影响了通过管壁传输的THz波的谐振特性,对比朝向为0°的光栅波导管与空白波导管的时域信号可以看出,其在第二个脉冲周期处有一个0.4 ps的延迟,如图6.11(a)所示。

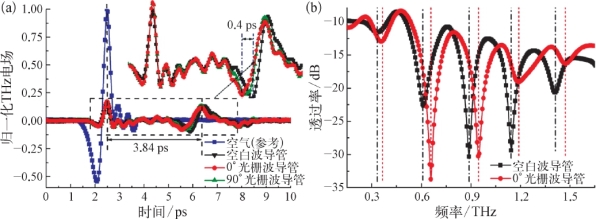
图6.11　

(a)实验测量得到的空气(参考)、空白波导管、0°和90°光栅波导管的THz时域信号;(b)实验测量得到的空白波导管和0°光栅波导管的透过率谱[8]

对以上所说的两个脉冲周期,由于有稳定的相位差,且偏振相同,因此可以发生干涉,在频域上表现为一系列等间距的谐振。理论上,这是一种典型的双光束干涉模型,当第一个脉冲与第二个脉冲的相位差达到π的奇数倍,也即通过空气传输与通过管壁传输的THz波的光程差达到λ/2的奇数倍时,干涉为相消干涉,在透射光谱上表现为谐振谷的出现,谐振谷所在的频率位置f m可以表示为

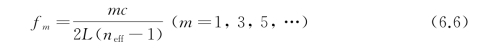
式中,m为谐振的级次;c为真空中的光速;2L(n eff-1)为光程差;n eff为光栅波导管的有效折射率。在此实验中,THz波聚焦在波导管的一端,因此对于透射的THz波来说,L=2d,其中d为管壁的厚度,d=1 mm。由式(6.6)可以得出两个相邻谐振的频率间隔Δf表示为(www.xing528.com)

实验测得的时域信号经过傅里叶变换后可以得到频域振幅信号,从而可以得到透过率谱,其计算公式为|P(ω)|=20lg(|E s(ω)|/|E r(ω)|),其中|E s(ω)|和|E r(ω)|分别是经过样品和经过空气参考光的振幅。由图6.11(b)可知,在0.34 THz、0.61 THz、0.89 THz、1.14 THz、1.41 THz处有明显的谐振,谐振宽度约为50 GHz,谐振频率间隔近似相等,均为0.27 THz左右。在时域上,两束THz波的光程差可以表示为

由图6.11(a)可知延迟时间为Δt=3.84 ps,所以由式(6.8)可以得到n eff=1.576,将这个n eff代入式(6.7)中可以得到Δf=260 GHz,这与实验测得的270 GHz非常接近,这是由于波导材料的色散使得Δt的值很难精确得到,事实上由于色散每一个频率位置对应的折射率是不同的。总之,通过式(6.6)可以精确得到频率f m处的有效折射率,但是由图6.11(a)中的延迟时间Δt及式(6.8)得到的n eff只是一个近似的平均值。

由图6.11(b)可知,在各个谐振频率处,空白波导管相对于光栅波导管有一个50 GHz的红移,这说明了光栅对波导管的谐振频率具有调制作用。当Δt=+1 ps时,对应的Δn eff=+0.15,而从图6.11(a)可以看出空白波导管和0°朝向光栅波导管在第二个脉冲周期有0.4 ps的时间延迟,故空白波导管的有效折射率n eff=1.576+0.06=1.636,这也和PMMA材料实际的折射率(约为1.6)接近。之所以空白波导管的谐振位置相对光栅波导管发生红移,是由于周期性的空气槽结构导致了光栅波导管管壁的相对折射率n eff减小,从而使得空白波导管比光栅波导管的f m值要小。综上可知,无论从时域还是频域角度分析,实验与理论的结果都非常吻合。

从图6.11(b)中可以看出,图中光栅波导管的第二级谐振Q值达到13,是空白波导管谐振Q值的2倍。在所有的谐振当中,第二级和第三级谐振有更高的Q值,因此后面主要讨论这两个谐振频率。