实验结果与理论分析对比分析

实验使用的硅光子晶体为三种不同几何结构：PC1和PC2为正方晶格,PC1的圆柱直径d=100μm,周期a=160μm;PC2的d=50μm,a=125μm;PC3为三角晶格,d=100μm,a=180μm。三种结构的柱高h=120μm。将光子晶体样品置于THz-TDS系统的焦点处,如图6.1所示,THz波垂直入射光子晶体周期性平面。测量的时域信号如图6.1所示,相比于参考信号,光子晶体将THz脉冲延迟并展宽,三个样品的信号也有明显不同。将时域信号做傅里叶变换,可以得到样品的透过率谱线,结果如图6.2所示。对于PC1,在0.87 THz处有一个明显的谐振谷,带宽100 GHz,在1.7 THz处存在第二个谐振谷,带宽200 GHz;对于PC2,第一个谐振谷移动到1.4 THz处,带宽100 GHz,可见随着几何结构的缩小,谐振频率向高频移动;PC3的第一个和第二个谐振谷的位置与PC1基本相同,但谐振强度和带宽与PC1正好相反。可见,不同的光子晶体结构导致不同的导模谐振位置和强度。

图6.1　THz-TDS系统测量参考和光子晶体样品的时域信号[1]

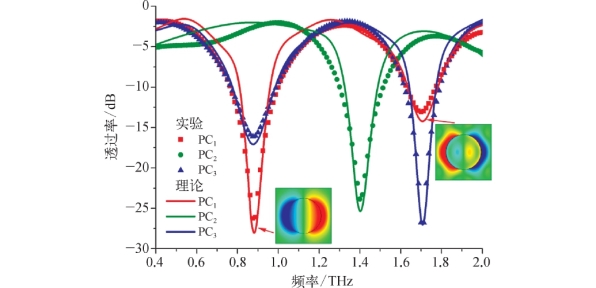
图6.2　通过实验和理论计算得到的THz光子晶体透过率谱线[1]

与过去报道的光子晶体平板孔阵列的导模谐振效应相比,光子晶体柱阵列的谐振谱线更为清晰和规则。导模谐振与光子带隙密切相关,因此这里首先计算了PC1和PC2两种结构的光子带隙,结果如图6.3所示。柱的高度是有限的,模拟的模型实际是一个三维结构,因此不同于光子晶体能带模拟,这里采用三维PWE方法进行数值求解。图6.3中纵坐标为归一化的频率,对于图6.3(a)中的PC1,a/λ=160/300=0.533对应着1 THz;对于图6.3(b)中的PC2,a/λ=125/300=0.416对应着1 THz,它们在图中的位置用绿线标出。由于光子晶体柱为有限高度,光子晶体柱外为空气(n=1),因此色散关系图中位于n=1的空气色散线(图中紫色曲线)之上的模式皆为泄漏模式,都不能在光子晶体周期平面内稳定传播而泄漏到空气中。空气色散线以内的模式为导模,不存在导模的频带即为光子带隙,图中由蓝色区域标出。实验测量得到的导模谐振的中心频率在图中用红线标出,PC1为0.466(对应0.87 THz),PC2为0.591(对应1.42 THz)。实验得到的导模谐振的中心频率正好对应着模拟计算的光子带隙的中心频率。当THz波进入光子晶体后,光子带隙阻碍着其频段内的THz波在光子晶体周期平面内自由传播,只能沿垂直周期平面方向谐振,由于带隙中部的Q值最高,导模谐振的中心频率位于带隙中部。因此,计算光子晶体的光子带隙可以有效判断导模谐振出现的频率,对器件设计有指导意义。

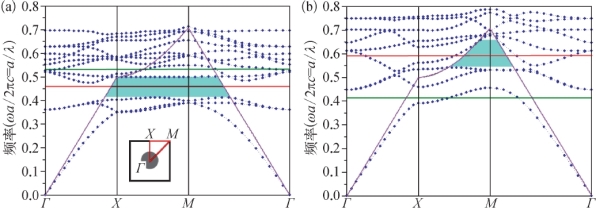
图6.3　PC1和PC2的光子能带图,其中蓝色部分为光子带隙,紫色为n=1的空气线,绿色线对应1 THz频率,红色线对应导模谐振的中心频率

(a)PC1;(b)PC2

光子晶体柱阵列的导模谐振是典型的偶极谐振。可见,THz光子晶体中的导模谐振效应是一种对原子系统中的偶极跃迁效应的模拟。过去在对光子晶体平板孔阵列的理论和实验研究中,其导模谐振的线形均由Fano谐振模型进行描述,Fano谐振是由Fano于1961年在原子光谱中发现的一种不同于Lorentz谐振的新型谐振[2,3],Lorentz谐振为对称线型,而Fano线型为非对称线型。然而,从图6.2可以看出,这里测试的光子晶体柱阵列的谱线是典型的对称线型,比光子晶体平板孔阵列的谱线更加清晰和规则,故有必要分析这两种几何上互补的结构的对称与非对称谱线的来源和相互关系。

此处的对称谐振谱线的电极化率χres(ω)用Lorentz模型来描述：

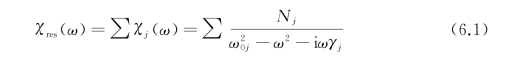(www.xing528.com)

式中,N j表示谐振强度。除了谐振项,模型中还应当包含一个由光子晶体组成材料决定的有效介电常数项εeff：

式中,f是各个材料占整个光子晶体空间的比例,这里特指硅和空气,它们的介电常数分别为εPC=εSi=11.7和εfill=εair=1。因此该结构的有效折射率n(ω)和相位ϕ(ω)表示为

在入射角度θ=0°时的振幅透过率t(ω)和功率P(ω)表示为

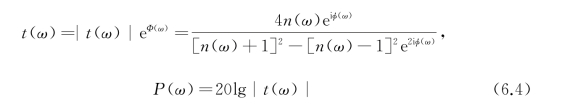
利用式(6.1)~式(6.4),可以计算得到三种光子晶体导模谐振的理论透射光谱线,如图6.2所示,所用的Lorentz模型的参数除了N 1是根据谐振强度拟合外,其余均直接取自实验测量结果,详见表6.1。从图6.2可见,式(6.1)~式(6.4)描述的理论谱线与实验结果吻合。

表6.1　光子晶体柱阵列Lorentz模型参数

上面讨论的整个传输系统是对称的,且光子晶体柱周围是空气,界面是匹配的,但在更普遍的情况下,当系统中引入一些非对称因子时,纯的Lorentz谐振将加上一个连续项,光有两条通过系统的传输路径：一条是伴随着法布里-珀罗(F-P)效应直接透射,另一条是由导模谐振引起的间接透射。直接与间接传输模式间干涉形成的谱线可以由Fano线型来描述[4,5]：

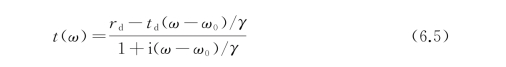
式中,t d和r d分别是直接传输模式的透射系数和反射系数,它们是Fano模型中的非对称因子;ω0是谐振频率;γ是谐振线宽。在一般情况下,t d≠1且r d≠0,谐振谱线是非对称的。当传输系统是对称的且F-P效应消失或可以忽略,即t d=1且r d=0时,则谱线将变为对称的。在光子晶体平板结构中,平板界面的折射率是失配的,F-P效应总是存在的,故先前报道的光子晶体平板的导模谐振均为非对称线形。而对于光子晶体柱阵列来说,在THz波正入射的情况下直接传输模式的F-P效应可以忽略,故谱线为对称线型。后面的实验将通过引入非对称因子来证明上述理论的正确性。