THz-TDS实验测试：橡胶基底的拉伸恢复特性和时域光谱曲线

如图5.35(a)所示,利用THz-TDS系统对橡胶基底进行了实验测试,插图为拉伸实验装置。图5.35(b)为橡胶、BCNTS20/橡胶和BCNTS60/橡胶的拉伸恢复特性的实验曲线,从图中可以看出橡胶基底具有很好的力学特性,其拉伸和恢复曲线基本一致,并且铺设CNT与否对它影响很小。

图5.35(c)为橡胶在0%、30%、60%、90%、120%和150%拉伸下的THz时域光谱曲线。从图中可以看出,随着拉伸程度变大,时域光谱曲线不断前移,而归一化的振幅峰值均保持在90%左右,这说明在拉伸过程中只有相位被调制而透过率没有变化。而相位的变化主要源于在拉伸过程中橡胶厚度不断变薄、光程不断减小。因此,可以把橡胶材料看成透明介质,在拉伸过程中它不会改变透过THz波的振幅和偏振态。

接着测试了BCNTS m/橡胶在CNT取向垂直和平行于THz波偏振方向(BCNTS⊥THz,BCNTS∥THz)时,不同拉伸程度下的THz时域光谱曲线,如图5.36所示。其中,BCNTS20/橡胶的时域信号如图5.36(a)和图5.36(b)所示,在拉伸程度从0%到150%的变化过程中不仅有相位的变化,而且振幅也随之改变。当BCNTS⊥THz时,时域信号的振幅随着拉伸程度的变大而增加,当BCNTS∥THz时,时域信号的振幅随着拉伸程度的变大而减小。如图5.36(c)和图5.36(d)所示,BCNTS60/橡胶也有类似的性质,只不过相较于BCNTS20/橡胶,它在时域上的振幅更小而已,这是由CNT本身的损耗导致的。总之,在BCNTS m/橡胶的拉伸过程中,THz波的振幅和相位均被调制。通过对时域信号进行傅里叶变换,可以得到对应的振幅透过率,如图5.37(a)和图5.37(b)所示。

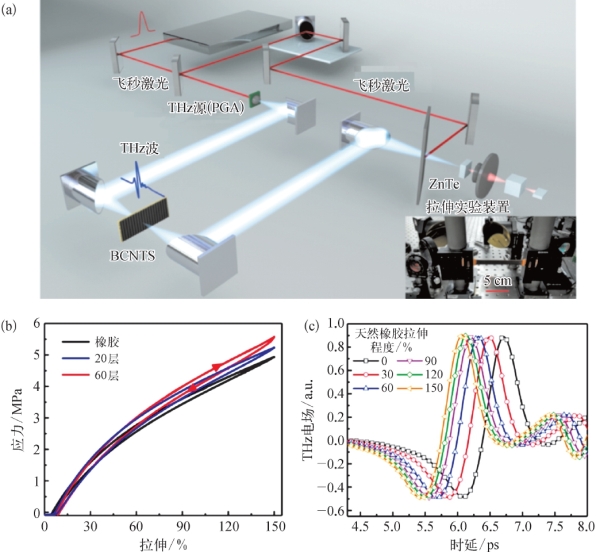
图5.35　

(a)THz TDS实验测试系统示意图,插图为拉伸实验装置;(b)橡胶、BCNTS20/橡胶和BCNTS60/橡胶的拉伸恢复特性的实验曲线;(c)橡胶在0%、30%、60%、90%、120%和150%拉伸下的THz时域光谱曲线[14]

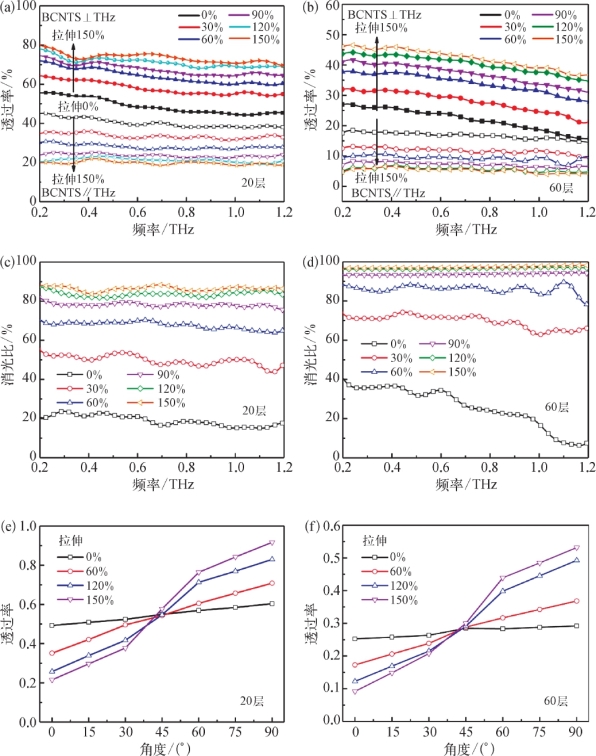
图5.37(a)为BCNTS20/橡胶在BCNTS⊥THz和BCNTS∥THz时不同拉伸程度下的振幅透过率曲线。当拉伸为0%时,BCNTS⊥THz时的透过率略高于BCNTS∥THz时的透过率,均在40%左右(在1 THz处分别为44.63%和39.29%);当拉伸程度变为150%时,BCNTS⊥THz时在1 Hz的透过率增至70.67%,而BCNTS∥THz时的透过率降至18.50%。BCNTS60/橡胶在不同拉伸程度下也有相同的变化趋势,只是其透过率整体低于BCNTS20/橡胶的透过率,如图5.37(b)所示。由此可见,BCNTS m/橡胶的透过率大小依赖于拉伸程度的变化,这意味着可以通过机械拉伸的方式实现器件偏振特性的主动调控。

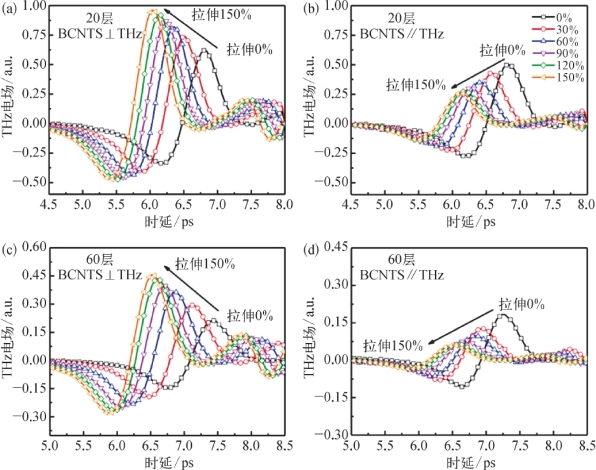
图5.36　THz波偏振方向分别垂直和平行于CNT取向时,样品在不同拉伸程度(0%～150%)下的THz时域光谱曲线[14]

(a,b)BCNTS20/橡胶;(c,d)BCNTS60/橡胶

为了研究BCNTS m/橡胶在不同拉伸程度下偏振度的变化,我们得到了它的消光比曲线,如图5.37(c)和图5.37(d)所示,计算消光比的公式如下：

式中,t⊥和t∥分别表示BCNTS⊥THz和BCNTS∥THz时的振幅透过率,对应的平方表示强度透过率。对于理想的偏振器来说,ER应该等于100%。对于BCNTS20/橡胶,当拉伸量从0%变化到150%时,在1 THz处ER从16.6%逐渐增加到88.3%;对于BCNTS60/橡胶,在1 THz时ER从17%增加到97%。这表明,CNT层数越多,对应的ER越高。然而CNT层数并不是越多越好,CNT层数越多,其整体透过率越低,如图5.37(a)和图5.37(b)所示。

(www.xing528.com)

图5.37　

(a,b)20层和60层在BCNTS⊥THz和BCNTS∥THz时不同拉伸程度下的振幅透过率曲线;(c,d)20层和60层的消光比曲线;(e,f)20层和60层不同拉伸程度和极化角度下的归一化透过率曲线[14]

此外,我们还研究了不同拉伸程度下,BCNTS m/橡胶的偏振特性随极化角度的变化,如图5.37(e)和图5.37(f)所示。BCNTS m/橡胶固定在一个角度可任意旋转的样品架上,由于光导天线产生的THz波为沿竖直方向的线性偏振光,因此旋转样品架可以改变入射THz波的偏振方向与CNT取向间的夹角。如图5.37(e)所示,BCNTS20/橡胶没有拉伸时,当极化角度从0°变化到90°时,其时域信号的峰值从49%缓慢上升至58%,并且峰值信号上升趋势随着拉伸程度的增大越来越显著。此外,当极化角度小于45°时,峰值透过率随着拉伸程度的增大而减小;当极化角度大于45°时,峰值透过率随着拉伸程度的增大而增大;当极化角度为45°时,峰值透过率恒定,接近0.5。这些实验结果表明,BCNTS m/橡胶能够实现从无拉伸时的各向同性态向拉伸150%时的各向异性态转变,即具有主动调控特性。

下面计算拉伸过程中BCNTS m/橡胶对THz波的调制率MD(f),计算公式如下：

式中,tε(f)、t 0(f)分别表示在ε%和0%拉伸程度下的振幅透过率,平方值表示其强度透过率。BCNTS m/橡胶在1 THz处的调制率如图5.38(a)所示,从图中可以看出在相同CNT层数m和拉伸程度ε%下,BCNTS m/橡胶在BCNTS⊥THz时的调制率要远远高于BCNTS∥THz时的调制率,并且它们都随着m和ε%的增加而单调增大。其中,在BCNTS⊥THz且ε%=150%时,调制率达到最大,约为365%。通过对比图5.35(c)和图5.36可知,BCNTS m/橡胶的相位变化主要来自橡胶基底厚度的改变。此外,调制率随着拉伸程度ε%的变化使得BCNTS m/橡胶可以用于拉力传感。为了表征它的传感性能,我们将调制率MD对ε的偏导定义为拉伸传感灵敏度SS,即

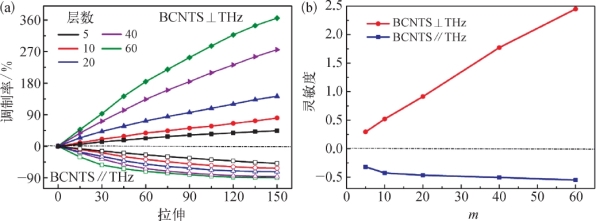
图5.38　BCNTS m/橡胶在m=5、10、20、40、60和BCNTS⊥THz、BCNTS∥THz时的调制率和灵敏度[14]

(a)调制率;(b)灵敏度

通过对图5.38(a)中调制率-应变曲线的拟合得到了BCNTS m/橡胶的平均拉伸灵敏度。如图5.38(b)所示,当BCNTS⊥THz时,其灵敏度随着层数m的增加从0.29线性增加到2.5,SS=2.5代表拉伸每改变1%,THz波的MD变化2.5%;当BCNTS∥THz时,其灵敏度随着层数m的增加从0.32增加到0.55。因此,拉力与ε%的关系以及调制率MD与ε%的相关性使得通过测量MD来推测拉力成为可能。

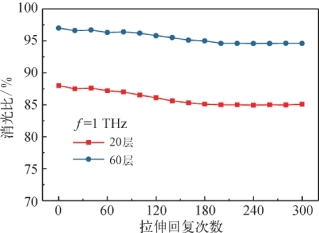
图5.39　BCNTS20/橡胶和BCNTS60/橡胶不同拉伸恢复次数下的消光比曲线[14]

为了说明BCNTS m/橡胶的鲁棒特性,对它在多次拉伸-恢复过程中的消光比进行了测量,如图5.39所示。总体而言,经过多次拉伸-恢复的循环,ER略有下降并最终趋于恒定,这说明BCNTS m/橡胶在多次工作后依然可以保持稳定的性能。