数值模拟与理论分析方法优化

为了更深入地分析和认识上面的实验现象和其中所包含的物理机制,依照图4.23和图4.24给出的几何和电磁参数进行数值建模,区域包括：空气折射率n=1,金属电极电导率σ=4.7×107 S/m,非掺杂GaAs(包括Si-GaAs基底和势垒耗尽层GaAs)和掺杂GaAs的介电常数如图4.23(b)所示。0 V、-15 V和15 V分别对应着不同的非掺杂和掺杂GaAs的区域分布,具体如图4.24所示。

用上述模型对不同正、负电压下的器件的传输谱线进行FDTD模拟,单元重复周期为10个,结果如图4.27所示,与图4.26所示的实验数据吻合较好。0 V时,在2.45 THz和3.25 THz处存在两个谐振峰;15 V时,前一个谐振峰跳变到2.3 THz,而后一个基本不变;-15 V时,前一个谐振峰基本不变只是强度略有减弱,而后一个随电压增大连续移动到2.9 THz处。这一模拟结果证实了器件的传输谱线随电压的变化与肖特基势垒宽度密切相关,其中跳变是由台阶肖特基势垒的变化引起的,而连续平移是由槽肖特基势垒的变化引起的。

图4.27　FDTD模拟的器件传输谱线[8]

(a)施加正向电压对应的台阶肖特基势垒宽度;(b)施加反向电压对应的槽肖特基势垒宽度

采用FEM算法对该器件模型的SPP模式色散关系与带隙图进行了计算,结果如图4.28所示。器件在-15 V和15 V、不同频率下模式的模场分布如图4.29所示。器件的周期性结构带来的布洛赫边界条件使得色散关系曲线弯曲,导模的群速度减小而成为慢光,群速度越小波导的微结构对导模的束缚和局域能力就越强,当群速度趋于0时,该模式成为束缚态而在金属-半导体界面上发生SPP局域共振,不能沿波导传播,形成光子带隙。图4.28中传播常数的实部(实线和点画线)表示导模,虚部(短虚线)表示束缚模式,对应着光子带隙。光子带隙越宽,SPP模式的局域性就越强,传输谱线中的谐振峰就越强。

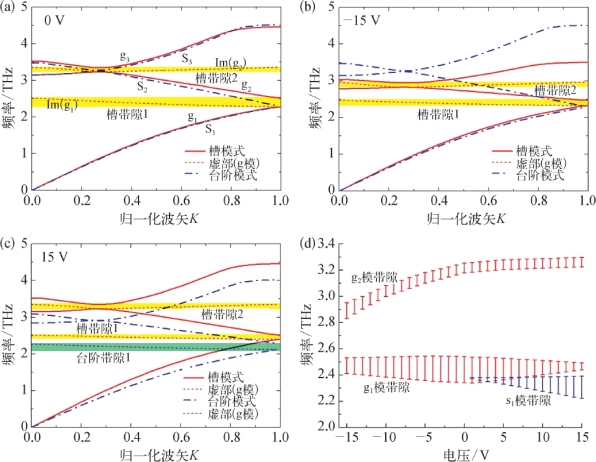
图4.28　器件模型的SPP模式色散关系与带隙图[8]

(a)0 V;(b)-15 V;(c)15 V;(d)光子带隙的频带范围随电压的变化(www.xing528.com)

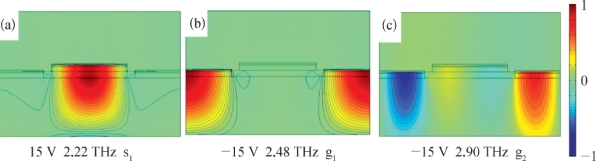
图4.29　器件在-15 V和15 V、不同频率下模式的模场分布[8]

如图4.28所示,该器件结构不同于普通SP波导或光子晶体波导,它是由两组不同的周期性金属-半导体表面等离子体栅阵组成的,它的能带关系图可以看作两组相对独立的SPP模式和色散关系曲线,其中一组SPP模式局域在台阶金属电极下,与台阶肖特基势垒的位置重合,它的色散关系曲线随着台阶肖特基势垒变化而变化(蓝色点画线);另一组局域在槽金属电极下,与槽肖特基势垒重合,它的色散关系曲线随着槽肖特基势垒变化而变化(红色实线)。为便于后文描述分别称为台阶SPP模式(s模)和槽SPP模式(g模),角标表示模式阶数。由图4.29的模场分布可以看出,由于SPP模场与肖特基势垒位置在空间上重合,器件电压所带来的肖特基势垒中载流子分布的空间调制,改变了SPP模场位置上材料的折射率和损耗的几何分布,这就引起其中的SPP模式及其光子带隙的变化。这种变化可以是带隙的产生、消失或移动,图4.28(b)和图4.28(c)显示了施加不同电压引起的两组带隙的分裂和移动,图4.28(d)显示了器件从-15 V到15 V时,各个带隙的动态变化过程。

0 V时,台阶和槽下方的肖特基势垒宽度相等、载流子分布情况相同,此时器件的能带结构和传输性质只由器件的结构决定。槽金属栅宽度为60μm,比台阶金属栅(50μm)略宽,两者间的几何结构的差异(包括栅宽和介质台阶)使得它们对SPP模式的束缚能力不同,因此SPP共振被激发并局域在槽肖特基势垒中形成光子带隙。如图4.28(a)所示,0 V时,两者对应的色散关系曲线差别很小,但槽肖特基势垒上的基模g1和二阶模式g2都存在光子带隙,带隙位置与实验数据相吻合,而台阶肖特基势垒上则没有光子带隙。

当施加电压时,肖特基势垒宽度变宽,由于势垒中GaAs的载流子浓度很低,其介电常数实部增大、虚部减小,对THz波的折射率增大、损耗减小,金属-半导体界面对SPP模式的束缚能力将增强,且SP波的特征频率ωsp及其色散关系曲线会向低频移动。这一结论可由半无限金属-电介质界面的SP波的特征频率公式定性地给出,半导体的介电常数εd增大,则ωsp减小。图4.28的模拟结果显示了施加正电压时,台阶模式的色散关系曲线向低频移动,而施加负电压时,槽模式的色散关系曲线向低频移动,且以上效应对基模(g1和s1模)的影响很弱,对高阶模式的影响则非常明显。

在施加正电压时,上述变化过程发生在台阶肖特基势垒上,而槽肖特基势垒会略微变窄。如图4.28(c)所示,随着电压增大,更多的能量耦合到台阶上,在2.2 THz附近s1模形成了对应的光子带隙,s1模带隙逐渐变宽,其谐振强度增大,而g1模带隙减小,谐振强度减弱,并趋于消失。因此,图4.26(a)和图4.27(a)中显示的谐振跳变源于台阶肖特基势垒一阶SPP模式的光子带隙的产生。

当施加负电压时,槽肖特基势垒变宽,槽金属栅的束缚能力进一步增强,因此束缚SPP模式依然在槽金属栅上被激发。这一过程中,如图4.28(b)所示,g2模的光子带隙随色散关系曲线从3.22 THz移动到2.87 THz。由于此时台阶肖特基势垒基本不变,台阶SPP模式不产生新的带隙。因此,图4.26(b)和图4.27(b)中显示的谐振连续平移源于槽肖特基势垒二阶SPP模式光子带隙的移动。还要注意到尽管s2模的色散关系曲线在施加正电压时也向低频发生类似的移动,但它没有产生新的光子带隙,如图4.28(c)所示。

本节主要介绍了一种基于双肖特基栅阵的THz调制器,实验结果表明,施加正向电压时,器件的谐振由2.48 THz处跳变至2.22 THz处,调制深度为15 dB,3 dB带宽为90 GHz;施加反向电压时,观察到谐振中心频率从3.22 THz到2.87 THz的平移,这一过程中强度调制深度为10 dB,3 dB带宽为75 GHz。通过实验测试和数值模拟证实了该器件结构存在的双等离子体光子带隙结构,施加不同电压可以控制台阶和槽金属电极下肖特基势垒中的载流子空间分布,从而控制势垒中THz SPP模式的光子带隙的产生和移动,实现对THz波的调制。这种高速、常温、低电压工作的特点使之便于与其他THz固态电子器件集成,是THz宽带无线通信技术发展迫切需要的器件。