THz亚波长介质光栅技术优化

1.亚波长介质光栅的传输与各向异性理论基础

图2.8　THz亚波长金属孔阵列结构及其振幅透射光谱线[8]

广义上的光栅包含二维的周期性柱阵列或孔阵列结构,是一类具有上百年研究历史的光学器件,其在衍射分光、色散补偿、全息变换等众多领域均有非常重要且历久弥新的应用。图2.9(a)为传统的衍射光栅,其栅格周期d大于入射光的波长λ。宽带入射光在经过衍射光栅之后会发生衍射,展现出显著的多级色散效应,其衍射场分布可以通过经典的基尔霍夫(Kirchhoff)衍射理论进行分析。亚波长光栅的栅格周期d小于或与入射光的波长λ相当。光在透过亚波长光栅传输时可能会出现多种光学异常效应,产生强烈的谐振和偏振相关响应,从而无法用经典的Kirchhoff衍射理论进行计算。如图2.9(b)所示,这些光学异常效应还导致亚波长光栅一般不产生像传统的衍射光栅那样的多级色散效应,对其透射场分布的计算应使用严格耦合波法。

图2.10为亚波长介质光栅结构示意图。其主要由基底层和介质光栅层组成。基底层的折射率为n 0,介质光栅层由折射率高低不同的两种介质构成,其折射率分别为n 1和n 2。一般情况下,基底层材料与高折射率介质光栅层材料相同,即n 0=n 1。介质光栅栅脊宽度为l 1,栅槽宽度为l 2,栅格周期为Λ,高折射率介质的填充系数为f,整体厚度为D,栅槽深度为d,对应入射光的波长为λ。

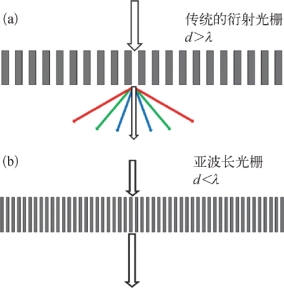
图2.9　

(a)传统的衍射光栅;(b)亚波长光栅

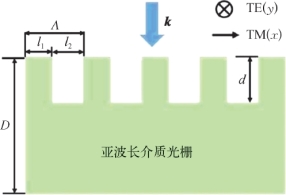
图2.10　亚波长介质光栅结构示意图,TE偏振方向沿着y轴,TM偏振方向沿着x轴,k为入射THz波波矢

类似于单轴晶体,设定光栅的栅脊方向为此单轴器件的主光轴,记作y方向,当光波偏振方向与主光轴方向成0°和90°时分别为TE模式和TM模式。

对于介质光栅结构,当栅格周期Λ远远大于入射光的波长λ时,衍射效应起主要作用。当栅格周期Λ小于入射光的波长λ时,零级衍射独立于介质光栅层的厚度和栅格周期,高阶衍射消失,此时介质光栅层可以等效为各向异性的媒质。这就是等效介质理论,下面详细介绍这一理论。(www.xing528.com)

当介质光栅为亚波长结构时,满足Λ≪(λ/n 1,λ/n 2),其中λ为入射THz波波长,n 1、n 2分别为两种填充介质的折射率。由于介层光栅层的折射率在一维x方向上周期性变化,x方向上的空间波矢k x为Bloch波矢。根据等效介质理论,对于TE模式,k x和z方向的波矢k z的关系满足式(2-24)。

亚波长介质光栅符合等效介质理论,因此其在THz波段可以类似于波片,具有相位延迟和偏振控制的功能,也可以用于定向发射。通常来说,非对称性的周期性表面单元结构可以为器件引入偏振相关的特性,使得器件具有类似于天然晶体一样的双折射效应。当两束偏振态相互正交的入射光通过器件后,会产生相位延迟。基于这种原理,我们可以利用亚波长介质光栅制备THz波段的相位延迟器或偏振转换器。

2.亚波长介质光栅的谐振效应

由于存在多种光学异常效应,亚波长介质光栅的透射光谱会出现一些奇特的现象,如瑞利异常、共振异常和非共振异常等。其中瑞利异常和非共振异常在传统衍射光栅中也经常出现,这里将更多地关注在亚波长介质光栅中经常出现的共振异常。在传输谱线中,共振异常一般表现为平滑而尖锐的谐振峰,如图2.11(b)所示,其通常是由光栅中的引导模式谐振或表面模式谐振引起的。引导模式谐振即导模谐振,如图2.11(a)所示。入射光在进入光栅内部后将在界面处发生多次反射,形成强烈的谐振,并转化为沿光栅内部传输的引导模式。由于光栅表面周期性结构的存在,这些引导模式并非一般介质光波导中传输的束缚模式,而是一种泄漏模式,在满足式(2.27)的相位匹配条件下可以与自由空间光发生耦合,并从光栅中泄漏出去。

式中,βGM为引导模式的波矢;k为反射光的波矢;θ为透射光的角度;m为常数,m=1,2,3,…;G为栅格的倒格矢,|G|=2π/d。当泄漏模式与直接反射光发生相长干涉,而与直接透射光发生相消干涉时,在器件的传输谱线上将出现明显的谐振峰。表面模式谐振与导模谐振的基本原理类似,一般在光与金属光栅相互作用时产生。当满足相位匹配条件时,光被耦合为表面等离子体模式,又可以从中解耦合出来,从而对传输性质产生影响。

图2.11　

(a)亚波长介质光栅中的导模谐振;(b)传输谱线中的瑞利异常和导模谐振

由于存在导模谐振,亚波长介质光栅表现出与传统衍射光栅截然不同的性质。在近场领域,由于泄漏模式和谐振效应的存在,在光栅表面附近将出现高强度的局域场。利用这一性质,将待测物放在光栅表面附近可以对其进行高灵敏度传感。而在远场领域,由于导模谐振产生的谐振峰具有很高的Q值,亚波长介质光栅可以被用来制备高性能的窄带滤波器。然而,在有些应用领域,导模谐振的存在将会对器件的传输性能和色散性质造成不良影响,因此需要极力避免。