探究THz表面等离子体效应

1.表面等离子体的理论基础

表面等离子体(Surface Plasma,SP)是由导体和介质分界面上的自由电子集体振荡产生的一种准静态电磁场模式,它强烈地局域在导体-介质表面并沿表面传播。如图2.4(a)所示,金属和介质的介电常数分别为εm和εd,电磁波沿无限宽金属-介质表面的x轴方向传播。电磁波有TM和TE两种偏振模式,将那些非零分量代入求解时谐电磁场的Helmholtz方程,并引入金属-介质界面上的连续性边界条件,可以得到TM波存在有意义的解：

因此,式(2.21)就是无限宽金属-介质上SP波的色散关系,而对TE波不存在物理上有意义的解,TE波不能激发SP波,SP波均为TM偏振波。

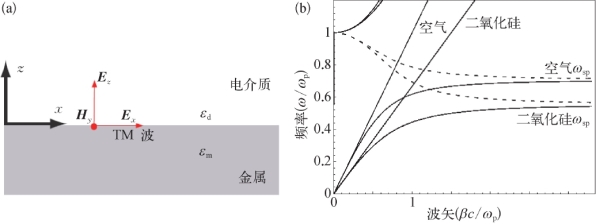
图2.4　无限宽金属-介质界面模型及其SP波的色散关系曲线[8]

图2.4(b)显示了在不考虑Drude模型中金属碰撞频率的情况下式(2.21)所描述的色散关系。当电磁波频率接近表面等离子频率时,传播常数β趋于无穷大,电磁波的群速度接近于0,这表明SP波强烈地局域在界面上成为强电磁谐振,这是SP波的根本特性。图中实线对应着β的实部,表示导模,而虚线对应着β的虚部,表示束缚和损耗模式,对应的频段也就是SP光子禁带。实际中金属都存在碰撞频率,即εm的虚部不为0,因此β不可能无限大,SP波沿界面向前传播并存在衰减。传播长度L=(2Im[β])-1描述SP波的有效传播距离,特征波长λsp=2π/Re[β]描述SP波在空间中的大小。

SP的重要应用是以金属材料和微纳米结构为基础的SP波导、透镜和传感器等。它可以形成亚波长结构的光子线路,并具有极高的灵敏度。此外,亚波长金属孔阵列的异常透射效应也与SP密切相关。

2.光学异常透射效应

1998年,Ebbesen等在研究电磁波与亚波长银膜圆孔阵列相互作用时得到了异常的透射光谱[9],如图2.5(b)所示。实验测试的圆孔阵列周期为900 nm,圆孔直径为150 nm,在稍大于周期尺寸的波长处,透射光谱中出现了明显的透过率峰。这些透过率峰的强度不仅大于圆孔相对于周期单元的归一化面积,甚至比Bethe等在1944年提出的经典小孔透射理论所求出的透过率高出若干个数量级。后者提出的经典小孔透射理论认为,光在透过无限薄金属板上的小孔时,其透过率可以由式(2.22)得到。

式中,T为透射率;D为小孔直径;λ为电磁波波长。透过率与这两者比值的四次方成反比,如图2.5(a)所示。然而,图2.5(b)给出的透射光谱在一些特定的波长处出现了和理论预期不相符的结果,金属孔阵列似乎起到了增强电磁波透射的作用,这种现象被称为光学异常透射(Extraordinary Optical Transmission,EOT)。

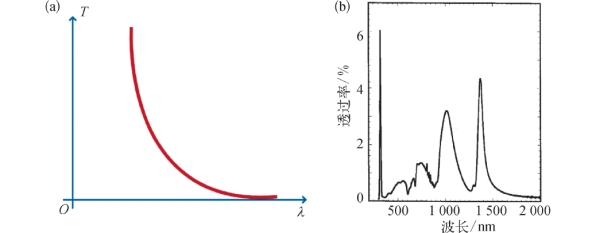
图2.5　(www.xing528.com)

(a)Bethe等提出的小孔直径与透过率的关系;(b)Ebbesen等获得的亚波长银膜圆孔阵列透射光谱[9,10]

EOT现象的发现极大地推动了亚波长人工微结构器件的发展。这是因为受制于传统的小孔透射理论,科研工作者在设计包含金属材料的亚波长微结构时往往会遇到透过率过低的困扰,而EOT现象则为这种困扰提供了解决的方法。随后,人们在红外、THz、微波波段都发现了EOT现象,并将其广泛地应用到了滤波、传感等领域。

在开发EOT现象潜在应用的同时,人们也对这种现象背后蕴藏的物理机理产生了浓厚的兴趣。目前对EOT现象较主流的解释有两种,分别是宏观Bloch模式和微观表面波模式。宏观Bloch模式将金属孔阵列结构看成一个整体,研究这个结构的表面模式对透射波的影响;微观表面波模式研究的结构单位是仅沿一个方向周期排布的单个孔链结构,考虑的是这个孔链结构激发的平整金属表面支持的表面波模式对透射波的影响。对于THz波段的EOT现象,前一种解释认为赝表面等离子体波增强了金属板结构表面的电场强度,从而提高了整体的透射率,而后一种解释则认为复合衍射倏逝波的存在导致了EOT现象。关于这两种解释的争论至今仍无定论。此外,还有人提出了基于复合波模式的解释,认为EOT现象是SP波和准柱面波共同作用的结果。综上所述,EOT是一种非常有趣而奇特的现象,对其深层次物理机理的研究更是意义非凡。

3.THz表面等离子体的特点

由上面的讨论可知,SP的共振频率ωsp与导体的等离子体频率ωp在同一数量级,由式(2.4)可知,ω2p正比于导体中的载流子浓度n。如图2.6所示,常见金属的载流子浓度在1023 cm-3量级,使得ωsp位于近红外与可见光波段,而THz波远低于这一频率,这就使得THz频率下β→k 0n,即THz SP波无法局域在金属-介质表面传播,其与自由空间中的THz波性质无异,因此简单金属-介质平面无法支持THz SP波。但是比金属载流子浓度低很多的半导体材料能够满足ωsp落在THz波段的要求。如图2.6所示,InSb的载流子浓度为1×1017 cm-3,它的表面可以支持THz SP波。

更重要的是,可以通过设计具有周期性人工微结构的金属或半导体表面,使它的有效介电常数所对应的ωsp落在THz波段,形成赝表面等离子体。它与无人工微结构的导体-介质表面的SP色散关系是相同的,在本书中不加以区别,统称为“表面等离子体结构”。如图2.7所示,它的THz传输及谐振性质与几何结构有关,而与金属材料性质无关,因此微结构表面等离子体波导成为重要的THz人工微结构器件。

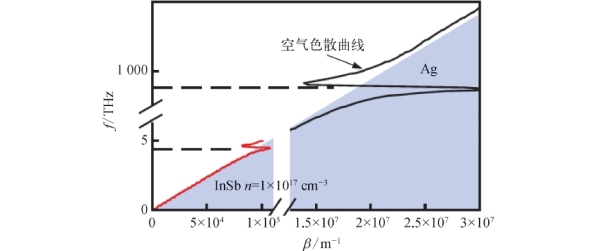
图2.6　THz波段SP的色散关系曲线[8]

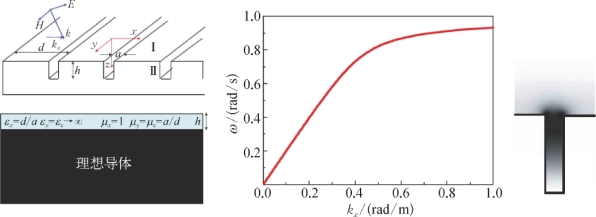
图2.7　周期结构SP波导结构模型和等效参数、色散关系,以及模场分布[8]

THz波段同样存在亚波长金属孔阵列的异常透射效应,当满足相位匹配条件时,一定频率的入射THz波能与SP波耦合形成谐振和增强传输,这一相位匹配条件为

式中,k sp是SP波波矢;k∥为入射THz波波矢在平行于周期阵列表面的分量;q为周期阵列提供的附加晶格矢量。若晶格周期为d,|q|=2π/d。图2.8所示为THz亚波长金属孔阵列结构及其振幅透射光谱线,它在1.46 THz处发生强烈的传输增强效应,其正入射振幅透过率远大于1。