主动波浪吸收的造浪技术优化方案

本节主要考虑主动式波浪吸收的造波控制方式，选取表7.1中浅水波条件T=2.3s及非浅水波条件T=1.4s的波况实例进行波浪水槽物理模型实验。对于浅水波条件T=2.3s的波况实例，除波高H=0.08m以外，分别应用改进的椭圆余弦波造波理论和近似流函数波造波理论、采用单信号模式和双信号模式进行实验，并与7.2.1单纯造波方式的定位模式实验结果进行比较。需要说明的是，应用改进的椭圆余弦波造波理论时双信号模式的控制信号考虑了色散修正和衰减模态的修正，这与近似流函数波造波理论中的处理方式相同。而采用单信号模式时，由于只有行进波的波面高程为所需提供的控制信号，色散修正和衰减模态的修正对于两种造波理论的单信号模式控制信号没有任何影响。对于非浅水波条件T=1.4s的波况实例，只应用近似流函数波造波理论，采用单信号模式和双信号模式进行模型实验对比验证。

图7.17和图7.18分别给出了T=2.3s、H=0.24m、h=0.4m波况应用改进的椭圆余弦波造波理论和近似流函数波造波理论采用单信号模式和双信号模式两种控制信号在水槽中得到的波面高程时间序列测量值与流函数波理论解（SF theory）的比较。与它们相对应的定位模式的实验结果参见图7.7和图7.8。

图7.17　T=2.3s、H=0.24m、h=0.4m时应用改进的椭圆余弦波造波理论采用主动波浪吸收方式的测量值与流函数波理论解的比较

对主动式波浪吸收的两种控制模式进行比较，双信号模式的优势相当明显。无论是改进的椭圆余弦波造波理论还是近似流函数波造波理论，单信号模式生成的波浪在水槽中波形不稳定，而且有波浪破碎的现象发生。反观双信号模式，两种造波理论的实验结果均比较理想，水槽中的波形均比较稳定。对于具有强非线性特性的该波况，近似流函数波造波理论的实验结果更具优势。

图7.18　T=2.3s、H=0.24m、h=0.4m时应用近似流函数波造波理论采用主动波浪吸收方式的测量值与流函数波理论解的比较

对双信号模式的实验结果与图7.7和图7.8中定位模式的实验结果进行比较，可见应用椭圆余弦波造波理论时双信号模式得到的波浪具有比较稳定的形态，而采用定位模式情况下波浪水槽中波形不稳定且出现了波浪破碎现象。需要说明的是，图7.7中应用的是传统的椭圆余弦波造波理论，即未考虑色散修正；图7.17中应用的是改进的椭圆余弦波造波理论，包含了色散修正，但对于该浅水波况色散修正的影响很小，因此两者具有可比性。定位模式效果不佳的原因如前所述，主要是由于椭圆余弦波造波理论对于强非线性波的描述不够准确造成。而采用双信号模式得到较好结果的原因主要是由于当造波理论对强非线性波效果不理想时，双信号模式根据控制系统要求的第二个控制信号，提供了对造波板运动位移信号进行适当修正的机会。对于该波况应用近似流函数波造波理论时，无论是定位模式还是双信号模式均得到了比较好的波浪生成效果。一个有趣的现象是，当采用单信号模式时，应用近似流函数波造波理论生成非线性波的实验结果反而比改进的椭圆余弦波造波理论的实验结果还要糟糕。其原因可能是由于与椭圆余弦波理论相比流函数波理论包含了更高阶的非线性特性，而单信号模式中主动吸收系统是在线性造波理论的基础上将特定的波面高程控制信号转换为造波板运动位移，主动吸收系统采用的线性特性导致了与预期流函数波理论的非线性特性更大的偏差。

图7.19给出了T=2.3s时不同波高条件下分别应用改进的椭圆余弦波造波理论（CN）和近似流函数波造波理论（SF）、采用三种不同控制方式在波浪水槽中三个测点处测得的波面高程时间序列与流函数波理论解（SF theory）相比较得到的相对误差ErrRMS，对应的相对误差ErrH如图7.20所示。图7.19和图7.20中的相对误差结果清晰地显示了应用近似流函数波造波理论、采用定位模式和双信号模式控制方式的优势，这也同时验证了两种主动波浪吸收方式中与单信号模式相比双信号模式的显著优势。

图7.19　T=2.3s波况实例的相对误差ErrRMS(www.xing528.com)

图7.20　T=2.3s波况实例的相对误差ErrH

应用改进的椭圆余弦波造波理论时，随着波高的逐渐增大，相对误差ErrRMS随之增大；另外当波高较大时，定位模式得到的相对误差ErrH在不同测点之间差异较大，而采用双信号模式的实验结果得到改善。

应用近似流函数波造波理论时，定位模式的效果始终比双信号模式的效果好。因此可以说，当造波板的运动位移控制信号与期望值吻合较好时，双信号模式系统中第二个控制信号没有起到修正的作用，反而带来了一定的扰动。尽管如此，双信号模式的最大优势是具有主动式吸收的非线性波浪生成，能够适用于存在较强反射性结构物的非线性波场。

图7.21给出了非浅水波况T=1.4s、H=0.20m、h=0.4m时应用近似流函数波造波理论采用单信号模式、双信号模式和定位模式三种不同控制信号在水槽中得到的波面高程时间序列测量值与流函数波理论解（SF theory）的比较。和所预期的一样，单信号模式生成的波浪效果比较差，定位模式和双信号模式生成的波浪测量结果与流函数波理论解吻合较好，与单信号模式相比优势显著。与双信号模式相比，定位模式的实验结果更好一些。主要原因是由于双信号模式中对运动造波板处波面高程的衰减模态修正是基于线性造波理论。图7.22给出了T=1.4s时不同波高条件下应用近似流函数波造波理论（SF）采用定位模式、单信号模式、双信号模式三种不同控制方式在波浪水槽中三个测点处测量值与流函数波理论解（SF theory）相比较得到的相对误差ErrRMS和ErrH。对于所有的波高实例，三种控制方式中单信号模式的相对误差均最大。双信号模式的相对误差ErrRMS和ErrH尽管与定位模式相比略微大一点，但是除了最大波高H=0.20m波况的ErrH较大（三个测量结果的平均值约10%）以外，其他波况的误差均相对较小，相对误差值≤5%。

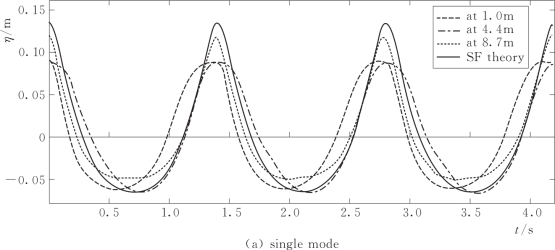
图7.21　（一） T=1.4s、H=0.20m、h=0.4m时应用近似流函数波造波理论采用不同控制方式的测量值与流函数波理论解的比较

图7.21　（二） T=1.4s、H=0.20m、h=0.4m时应用近似流函数波造波理论采用不同控制方式的测量值与流函数波理论解的比较

图7.22　T=1.4s波况实例应用近似流函数波造波理论的相对误差ErrRMS和ErrH