斜向流函数波实例演示

现在转移到应用斜向流函数波理论进行与第6章6.2.2相同的过程。为求解式（6.26）的造波板运动位移，η（x，y，t）依据流函数波理论[6，7]得到下列形式的表达式：

式中：Aj为已知波浪的相关常数，j=1，2，…，N。

图6.14　H=0.12m条件下椭圆余弦波和流函数波理论得到的X（y，t）比较

采用与第6章6.2.2相同条件对控制信号进行数值求解。图6.14给出了H=0.12m波况条件下应用椭圆余弦波（CN）和流函数波（SF）分别得到的色散修正后造波板运动位移X（y，t）的比较，是通过y=Ly处X（Ly，t）的时间序列以及t=T时刻X（y，T）剖面之间的比较来体现。流函数波得到的X（y，t）振幅比椭圆余弦波的结果小一些，这与波浪水槽中的现象（图5.11）一致。另外，由流函数波得到的X（y，t）沿y方向的波长比椭圆余弦波的波长略长，由此得到了不同的相速度，椭圆余弦波给出的向速度为c=1.948m/s，流函数波给出的向速度为c=1.937m/s。

对于双信号模式，利用衰减模态修正得到预期波面高程ηI，0（y，t）。图6.15给出了H=0.12m条件下应用椭圆余弦波（CN）和流函数波（SF）得到的ηI，0（y，t）之间的比较，同样是通过y=Ly处ηI，0（Ly，t）的时间序列及t=T时刻ηI，0（y，T）剖面之间的比较来反映。流函数波理论给出的波峰和波谷值均比椭圆余弦波的波峰和波谷值略大，此外由于相速度不同导致流函数波理论得到的ηI，0（y，T）沿y方向波长比椭圆余弦波略小。

图6.15　H=0.12m条件下椭圆余弦波和流函数波理论得到的ηI，0比较(www.xing528.com)

应用三维流函数波波浪生成的控制信号进行上述斜向非线性规则波的物理模型实验。图6.16给出了H=0.12m波况三种不同控制模式和H=0.20m波况定位模式的波面高程测量结果分别与流函数波理论解（SF theory）的比较。与图6.11所示的应用三维线性造波理论结果相比波浪生成的效果改善很多，但是与图6.12所示的应用椭圆余弦波理论的结果类似，没有明显改善。采用三种不同控制模式均捕捉到了非线性波的一般形态。双信号模式和定位模式生成的斜波比单信号模式的效果好些，然而在物理波浪水池中波形不太稳定，测量结果的相对误差如图6.17所示。

图6.16　（一） 应用三维流函数波理论的测量结果与流函数波理论解的比较

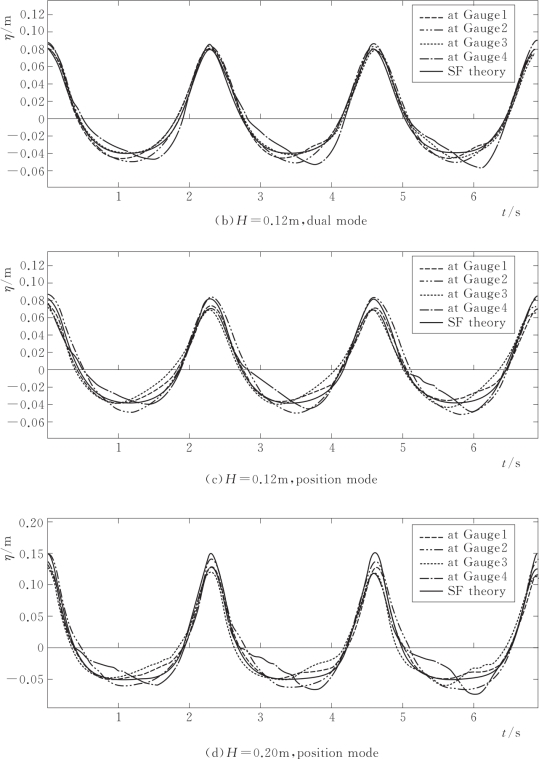
图6.16　（二） 应用三维流函数波理论的测量结果与流函数波理论解的比较

图6.17　应用三维流函数波理论的测量结果相对误差

在第5章波浪水槽的实验中，应用流函数波作为特定统一造波理论输入的实验结果与应用椭圆余弦波作为输入的实验相比改善很多，近似流函数造波理论的优势显著。然而对于波浪水池的斜向波非线性波实验，应用三维流函数波作为输入的优势不再明显。可能的原因包括：造波理论在色散修正和衰减模态修正均基于线性理论；测量系统中浪高仪校准因子的准确性；物理模型实验中静止水面的干扰、微小的水深变化等。这些原因均会产生不同程度的误差，但是主要的原因可能是由于三维推板式造波机的单推板宽度（dy=0.5m）引起。对于强非线性波的波浪生成来说0.5m的空间步长太大。比如，波况条件为H=0.12m、h=0.4m、T=2.3s、α=45°时，流函数波理论得到的y方向波长为Ly=6.29m，固定的dy=0.5m空间步长确定了每个主谐波的波长只有13个网格点，而更高阶谐波步长上的网格点分布更少。此外板前的线性分段特性也会造成波浪非线性的不连贯。

因此，可以认为应用椭圆余弦波理论或流函数波理论联合应用特定统一造波理论能够成功地在波浪水池中生成斜向非线性波。在波浪水池中难以获得强非线性波稳定波形的主要原因是由于设备本身推板宽度的限制。可以预见，当推板宽度足够小时，三维流函数波理论联合应用特定统一造波理论能够得到如水槽中强非线性波浪生成实验那样比较理想的结果。