线性斜波实例演示

首先对线性全色散斜波进行实验，采用线性波浪理论。平底水深h=0.7m条件下波浪要素为波高H=0.05m，周期T=1s，波向α=45°。由此得到相对水深kh=2.83，其中k为波浪传播方向的波数；y方向的波长为Ly=2.195m。依据线性波浪理论：

为了计算浅水条件下造波板运动位移，对式（6.18）进行线性化处理。用造波板平均位移处的速度替代造波板运动位移处的速度，同时略去左侧第二项的非线性项。此外，为了避免产生第3章3.3.2中讨论过的偏移问题，采用如下斜坡函数fr（t）对U（x，y，t）进行修正：

由此，式（6.18）转化为

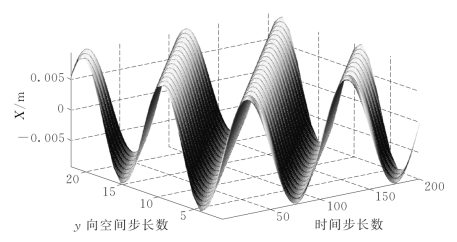
其中，x0为造波板平均位移的位置，选取ωc=2π/30Hz以及Tr=15s。随后依照式（6.19）进行色散修正。应用显式中心差分格式对其进行离散并进行数值求解，空间步长取为dy=0.2m，时间步长取为dt=0.01s。色散修正后预期的造波板运动位移如图6.3所示。图6.4给出了色散修正前后Xsw（Ly，t）和X（Ly，t）之间以及Xsw（y，T）和X（y，T）之间的比较，可见色散修正的影响比较显著。

采用双信号模式控制系统时，需要运动造波板处的波面高程信号。根据波浪的线性特性，由式（6.20）可得到X=0处行进波部分的波面高程。衰减模态修正部分的波面高程由式（6.21b）计算得到，如图6.5所示。

(www.xing528.com)

图6.3　预期的造波板运动位移X（y，t）（dy=0.2m，dt=0.01s）

图6.4　色散修正前后Xsw和X的比较

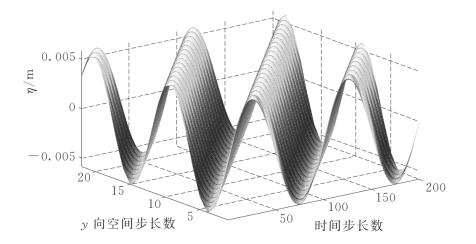
图6.5　衰减模态的波面高程（dy=0.2m，dt=0.01s）

基于三维线性波浪理论及造波理论，得到造波板运动位移和衰减模态波面高程的理论解：

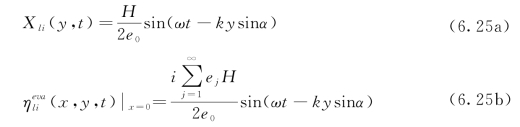
由本例的波浪条件可知，对造波板运动位移的计算结果X（y，t）和理论解Xli（y，t）进行比较，按照式（5.30）定义的相对误差ErrRMS（y）和ErrH（y）的最大值分别为0.10%和0.19%。同样对衰减模态波面高程的计算值和理论值进行比较，最大的ErrRMS（y）和ErrH（y）分别为0.02%和0.07%，由此验证了特定统一造波理论对线性斜波实例的有效性。