生成线性波浪的方法及应用

依据三维全色散线性造波理论，造波板运动位移幅值与对应行进波的波面高程幅值之间的关系式如下：

其中，e0为传递函数，其定义为

此外，B表示行进波水深平均速度x分量的复式傅里叶幅值，由此可得

由式（6.4）和式（6.6）消除AI（ω）可得

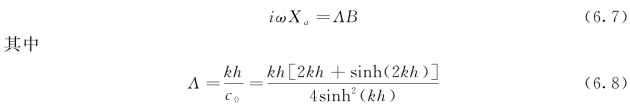
式（6.8）的传递函数Λ与用于二维波浪水槽的式（5.8）完全一致（图5.1）。这表明传递函数Λ与波浪的传播方向无关。因此在时域内的造波板运动位移可按照第5章5.1.1中介绍的方式进行求解：

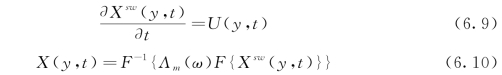
式中：F和F-1分别为关于时间t的傅里叶变换和傅里叶逆变换；Λm（ω）为改进后的传递函数，如图5.1所示。

采用双信号模式的主动式波浪吸收方法时，还需要运动造波板处的波面高程控制信号。由于造波板前衰减模态波场的产生，有必要对行进波的波场进行衰减模态修正。根据线性造波理论可得

式中：ej的定义见第2章2.2.4中式（2.40）。(www.xing528.com)

图6.1　衰减模态修正传递函数Γ

图6.1给出了二维传递函数Γ（ky，ω）随无量纲化的波数和角频率变化的情况。图中既包括了（沿造波板方向的波长大于或等于行进波的波长）的情况，同时也包括了（沿造波板方向的波长小于行进波的波长）的情况。图6.1中的曲线给出了时的临界值，行进波的情况对应图中临界曲线的右下侧部分。由于造波设备对频率的限制以及MIKE 21 BW对水深适用条件的要求（kh＜3），采用式（5.11）的衰减函数fd（ω）和与其类似的fd（ky）对二维的传递函数Γ（ky，ω）进行改进，改进后的传递函数Γm（ky，ω）表达式如下：

式中fd（ky）定义为

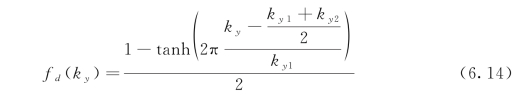
其中，ky1和ky2是与kyh的最大值相关的两个参数，考虑到MIKE 21 BW的水深适用条件，在此选取ky1h=4和ky2h=5。

图6.2给出了改进后的衰减模态修正二维传递函数当波浪为正向波时，二维传递函数Γm与图5.4所示的一维传递函数Γm完全一致。

图6.2　改进后的传递函数Γm

在物理空间内运动造波板处的波面高程表达式如下：

式中分别为二维傅里叶变换和二维傅里叶逆变换。