实例：不规则波的变水深传播

为了验证不规则非线性波确定性联合模拟的效果，选取不规则波从深水爬坡至浅水平台的实例进行模型实验。复合模型示意如图5.33所示。整个复合模型的波浪水槽长度为160m，数学模型中入射波在2.6m水深处开始爬坡，底部坡度为1∶50，直至水深0.4m浅水平台。不规则入射波采用标准的JONSWAP波谱[9，10]，有效波高Hm0=0.12m，峰波浪周期Tp=3s，谱型参数为γ=3.3，σa=0.07，σb=0.09。最小波周期取为Tmin=2.6s，数值模拟的时间步长取为dt=0.01s，空间步长取为dx=0.1m。图5.34所示为数学模型计算结果中提取的t=180s时刻在水深0.4m浅水平台处的P通量和波面高程（η）沿x方向变化的剖面图，可见波浪经过浅水变形后成为不规则非线性长波。

图5.33　复合模型示意图

图5.34　t=180s时刻h=0.4m处P通量和波面高程η沿x方向的剖面图

物理模型设置在水深0.4m的平底浅水区，布置两个固定的浪高仪用来测量波面高程，浪高仪在整个复合模型的位置为x1=128.2m和x2=131.6m。在整个复合模型的波浪水槽中设定两个不同的造波板平均位移的位置x0=125.2m和x0=127.2m用于数学模型和物理模型之间的数据传递及物理模型实验。

首先在复合模型的波浪水槽中设定造波板平均位移的位置为x0=125.2m，选取数学模型中t=60s时刻作为数学模型与物理模型之间数据传递的起始时刻，图5.35给出了数学模型计算结果中提取出的x0处波面高程和水深平均速度（U）的某一时段的时间序列。

图5.35　x0=125.2m处数学模型计算的波面高程和沿水深平均速度时间序列

本例中选取ωc=2π/20 Hz用于高通滤波，整个模型模拟时长为10min以计算造波板运动位移。图5.36给出了特定时段内的浅水条件下Xsw（t）与色散修正后预期值X（t）的比较，两者间最大偏差为0.0036m，发生在X（t）=0.253m时。可见偏差足够小，使得色散修正可以被忽略，这与非线性长波的实际情况一致。

图5.36　x0=125.2m时浅水条件下Xsw（t）与色散修正后预期值X（t）的比较

(www.xing528.com)

图5.37　不规则波运动造波板处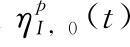）与造波板平均位移处ηI（x0，t）的比较（变水深）

对双信号模式的另一控制信号进行计算，图5.37给出了特定时段内不规则波运动造波板处行进波部分的波面高程与造波板平均位移处行进波的波面高程ηI（x0，t）的比较，当非线性较强时两者存在一定的差异，偏差最大值为0.0093m。该时段内造波板处不规则波行进波部分波面高程衰减模态部分波面高程及预期的总波面高程ηI，0（t）的比较见图5.38。与相比，衰减模态部分）非常小，所有本例中衰减模态修正的影响可以忽略不计，这与浅水波的实际情况一致。

采用上述计算的控制信号进行双信号模式的物理模型实验。当设定复合模型波浪水槽中造波板平均位移的位置为x0=125.2m时，物理波浪水槽中布置的两个浪高仪距离造波板平均位移分别为3.0m（Gauge1）和6.4m（Gauge2）。图5.39和图5.40分别给出了特定时段内Gauge1和Gauge2处的波面高程测量值（dual mode）与MIKE 21 BW数值解（BW）的比较。尽管测量值与数值解存在一些偏差，尤其是在波高较大时，考虑到波浪的强非线性特性，总体上物理模型的测量结果与MIKE 21 BW的数值计算结果吻合较好。在给定的Hm0和Tp条件下的Ursell数为71，波列中最大波高时的Ursell数会大很多。另外，在物理波浪水槽中浪高仪的下游有波浪破碎现象发生，而数学模型中未考虑波浪破碎。当波浪非线性特性较弱时，物理模型结果与数学模型结果的偏差较小。Gauge1和Gauge2处两个模型测量结果在整个模拟时长内最大相关系数分别为0.947和0.941。

图5.38　不规则波运动造波板处波面高程（变水深）

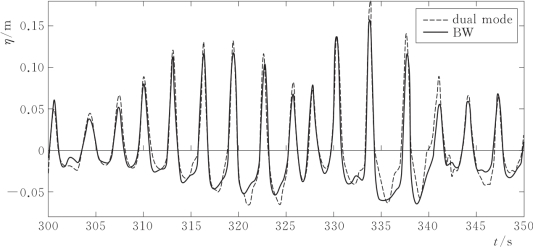
图5.39　x0=125.2m时Gauge1处波面高程测量值与数值解的比较

图5.40　x0=125.2m时Gauge2处波面高程测量值与数值解的比较

将复合波浪水槽中造波板的平均位移位置移动2m至x0=127.2m进行重复实验，因此在复合波浪水槽中固定的两个浪高仪在物理水槽中距离造波板平均位移分别为1.0m（Gauge1）和4.4m（Gauge2）。图5.41给出了特定时段内Gauge1和Gauge2处的波面高程测量值（dual mode）与MIKE 21 BW数值计算结果（BW）的比较，测量值与计算结果吻合良好，在整个模拟过程中Gauge1和Gauge2的最大相关系数分别为0.942和0.948。

图5.41　x0=127.2m时波面高程测量值与数值解的比较