不规则波在平底水深传播的实例分析

为了验证色散修正和衰减模态修正，下一步针对水深较深的不规则波进行实验验证。整个复合模型的波浪水槽长度为160m，平底水深h=0.7m，不规则入射波采用标准的JONSWAP波谱[9，10]，有效波高Hm0=0.05m，峰波浪周期Tp=1.2s，谱型参数为γ=3.3，σa=0.07，σb=0.09。考虑到数学模型MIKE 21 BW的精度要求，最小波周期取为Tmin=0.95s。由此可知不规则波的相对水深kh介于2.02和3.13之间。数值模拟的时间步长取为dt=0.01s，空间步长取为dx=0.1m。对于不规则波，由于波面高程和水深平均速度的时间变化过程与水槽中的位置有关，复合模型中数学模型与物理模型间的数据传递以及物理模型的造波板运动位移时间序列取决于造波板平均运动位移在水槽中的位置。因此，在整个复合模型的波浪水槽中设定两个不同的造波板平均位移的位置x0=96m和x0=99m用于数学模型与物理模型间的数据传递，x0即为物理波浪水槽中造波板的平均位移。另外布置两个固定的浪高仪用来测量物理模型中的波面高程，浪高仪在整个复合模型中的位置为x1=100m和x2=103.4m。图5.23给出了复合模型示意图。由于对不同的x0数据传递和计算处理过程完全一致，在此以x0=96m为例对过程进行描述。

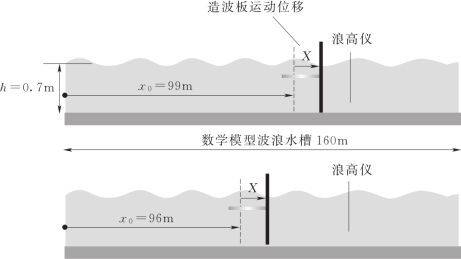
图5.23　复合模型示意图

首先设定物理模型中造波板平均位移的位置为x0=96m，选取数学模型中t=250s时刻为数学模型与物理模型间数据传递的初始时刻，图5.24给出了数学模型计算结果中提取出的x0位置处波面高程η（x0，t）和水深平均速度U（x0，t）的某一时段的时间序列。

图5.24　x0=96m处数学模型计算的波面高程和水深平均速度的时间序列

为了计算造波板运动位移，对数学模型计算结果P通量进行零均值修正以消除数学模型造成的误差，由此式（5.25）改写为

本例中选取ωc=2π/10 Hz用于高通滤波，整个模型模拟时长为10min。图5.25给出了与图5.24对应时段的浅水条件下Xsw（t）与色散修正后预期值X（t）的比较，色散修正前后Xsw（t）与X（t）之间的差异比较显著，需要说明的是图中时间坐标与数学模型的时间一致。

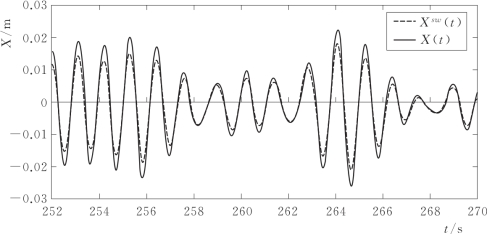
图5.25　浅水条件下Xsw（t）与色散修正后预期值X（t）的比较

为了应用双信号模式控制系统，图5.26给出了该时段内不规则波运动造波板处行进波部分的波面高程与造波板平均位移处行进波的波面高程ηI（x0，t）的比较，两者差异几乎为零，表明了波浪的线性特性。图5.27给出了该时段内不规则波运动造波板处行进波部分波面高程衰减模态部分波面高程）及预期的总波面高程ηI，0（t），衰减模态修正的影响比较显著。

图5.26　不规则波运动造波板处与造波板平均位移处ηI（x0，t）的比较（平底水深）

(www.xing528.com)

图5.27　不规则波运动造波板处不同波面高程比较（平底水深）

由于双信号模式与另外两种波浪生成的控制模式相比具有显著优势，在本例中采用上述计算的控制信号进行双信号模式的物理模型实验。在物理波浪水槽中布置两个浪高仪，距离造波板平均位移分别为4.0m（Gauge1）和7.4m（Gauge2）。图5.28和图5.29分别给出了特定时段内Gauge1和Gauge2处的波面高程测量值（dual mode）与MIKE 21 BW数值解（BW）的比较，测量值与数值解吻合较好。

图5.28　x0=96m时，Gauge1处波面高程测量值与数值解的比较

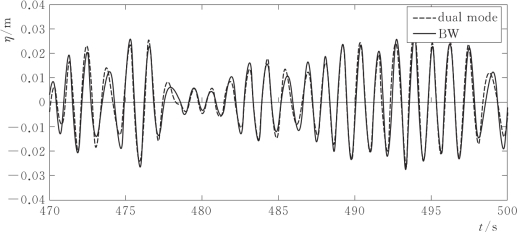
图5.29　x0=96m时，Gauge2处波面高程测量值与数值解的比较

图5.30　x0=96m时，Gauge1处测量值与数值解（dual mode&BW）的相关系数函数以及数值解的自相关系数（target auto）的比较

为了定量分析不规则波的误差，按照式（5.37）计算波面高程测量值与数值解在整个模拟时长10min内的相关系数函数ρxy（τ）。以Gauge1处的测量结果为例，图5.30给出了波面高程测量值与数值解的相关系数函数以及数值解的自相关系数的比较。在滞后时间τ=0时的测量值与数值解的相关系数函数（dual mode&BW）达到最大值为0.987，接近于数值解的自相关系数（target auto）最大值1。而且，相关系数函数的变化过程与数值解的自相关系数变化过程吻合良好，这表明了测量值与对应的目标数值解同步。Gauge2处的测量值与数值解最大相关系数为0.968，同样接近于1且发生在滞后时间为0的时刻。由此可见，本例中数值波浪的不规则波被非常好地传递至物理波浪水槽中。另外，注意到在Gauge1处的测量结果与数值解的吻合程度比Gauge2略好一些，主要原因是Gauge1更靠近造波机，误差相对小些。

现将复合波浪水槽中造波板的平均位移位置移动3m至x0=99m，为了使两个浪高仪在复合波浪水槽中位置固定，在物理波浪水槽中浪高仪距离造波板平均位移则分别变为1.0m（Gauge1）和4.4m（Gauge2）。图5.31和图5.32分别给出了特定时段内Gauge1和Gauge2处的波面高程测量值（dual mode）与MIKE 21 BW数值计算结果（BW）的比较，测量值与计算结果吻合良好。物理模型实验结果与数学模型计算结果在Gauge1和Gauge2的最大相关系数分别为0.994和0.985，均非常接近于1。需要说明的是，由于浪高仪的位置在复合波浪水槽中位置固定，因此图5.28和图5.31中Gauge1处的目标值MIKE 21 BW数值计算结果（BW）完全相同，同样的，图5.29和图5.32中Gauge2处的目标值（BW）完全一致。

图5.31　x0=99m时，Gauge1处波面高程测量值与数值解的比较

由此可见，所有在物理波浪水槽中的测量结果与数学模型计算结果均吻合良好。尽管物理波浪水槽中浪高仪距离造波板平均位移越近，测量结果与数学模型计算结果相比较的误差越小，但总体上，复合模型并不依赖于造波板平均位移的位置，因此复合模型对物理模型接替数学模型的具体位置不敏感。

图5.32　x0=99m时，Gauge2处波面高程测量值与数值解的比较