生成线性波浪的方法优化

在水平的波浪水槽情况下，依据第2章的全色散线性造波理论，造波板运动位移幅值与对应的行进波波面高程幅值之间的关系式为

其中，虚数单位i表明两者之间存在90°的相位差。对于推板式造波机，有Biesel传递函数c0的表达式：

B表示水深平均速度的复式傅里叶幅值，由质量守恒可得

由式（5.4）和式（5.6）消去AI（ω）可得

式（5.7）与式（2.53）完全一致。Λ可视为色散修正的传递函数。应用下列行进波的全色散关系式，可以得到传递函数Λ与角频率ω之间的关系，图5.1所示为传递函数Λ随无量纲化的角频率变化的情况。

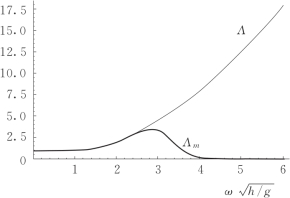
图5.1　色散修正传递函数Λ和改进后的传递函数Λm随无量纲化角频率的变化

由于波浪物理模型的造波设备通常对造波板运动的频率有一定的限制，传统上选取最大频率为2.5 Hz，即满足f≤fmax=2.5 Hz。另外考虑波浪数学模型应用的精度条件，比如，MIKE 21 BW的Boussinesq模型的水深适用条件为kh≈3，即，采用衰减函数fd（ω）对传递函数Λ进行改进，用改进后的传递函数Λm来替代Λ以达到抑制高频响应的目的。

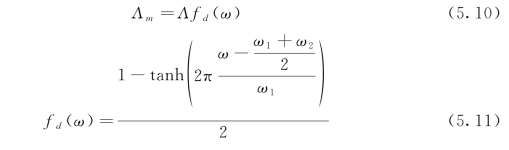
其中，ω1和ω2是与min（2πfmax，相关的参数。

假设最大的适用频率是由数学模型的精度决定，即设备的限制频率高于Boussinesq模型的限制频率此外，选取得到衰减函数随无量纲化的角频率变化的情况，如图5.2所示的改进后的传递函数Λm与Λ的比较见图5.1。当频率趋近于0（kh→0）时，Λm与Λ均趋近于1，因此在浅水限制条件下色散修正消失。

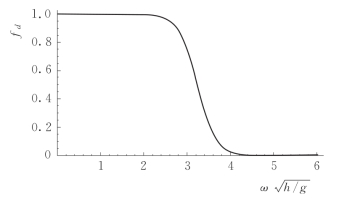
图5.2　衰减函数fd随无量纲化角频率的变化

式（5.7）可以重新写成两个方程的形式：

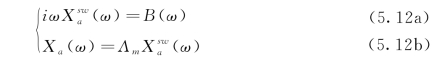
其中，上标“sw”表明应用浅水波浪理论根据造波板平均位移位置处水深平均的速度得到造波板运动位移。式（5.12b）给出了色散修正过程以摆脱浅水条件的限制。

造波板运动位移在时域内的求解过程可表述为

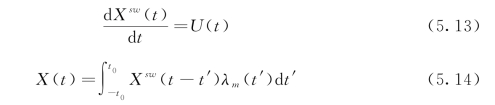(www.xing528.com)

式（5.14）的色散修正过程是通过卷积定理来实现的。式中，λm（t）为对应于改进后色散修正传递函数Λm（ω）的脉冲响应函数，如图5.3所示。t0反映了脉冲响应函数的有效宽度。脉冲响应函数的无量化有效半宽这表明色散修正的脉冲响应函数λm（t）只是在局部产生影响。

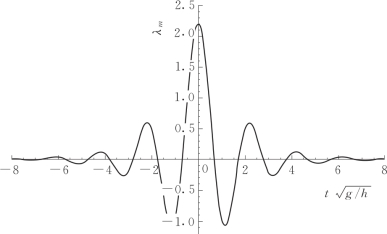
图5.3　色散修正的脉冲响应函数λm（t）

在实际应用中，首先利用离散的（ω）和Λm（ω）在傅里叶空间进行色散修正，之后再通过离散傅里叶逆变换用离散卷积的形式得到造波板运动位移，其表达式如下：

其中，F和F-1分别表示傅里叶变换和傅里叶逆变换。式（5.15）与式（5.14）具有相同的色散修正效果。

采用双信号模式的主动式波浪吸收方法时，运动造波板处的波面高程是另一个必需的控制信号。由于造波板的形态与行进波水平速度的垂直剖面之间的不匹配会造成造波板前衰减模态波场的产生，因此，有必要对行进波的波场进行衰减模态修正。由式（4.11）和式（2.44）可得

对于二维波浪水槽，衰减模态修正的传递函数Γ为

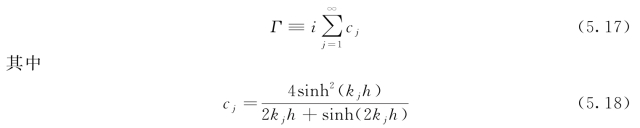
式中kj满足下列复式波数的线性色散关系：

图5.4所示为考虑衰减模数为20的情况下的传递函数Γ以及改进的传递函数Γm。类似于传递函数Λ的改进，为了抑制高频响应，同样采用衰减函数fd（ω）对传递函数Γ进行改进，用改进后的传递函数Γm来替代Γ。

当频率趋近于0（kh→0）时，Γm与Γ均趋近于0，因此在浅水的限制条件下衰减模态修正自然消失。

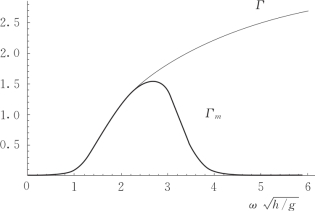
图5.4　衰减模态修正传递函数Γ和改进后的传递函数Γm随无量纲化角频率的变化

时域内运动造波板处的波面高程可表示为

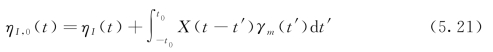
其中，γm（t）为对应于改进后衰减模态修正传递函数Γm（ω）的脉冲响应函数，如图5.5所示。t0可根据色散修正传递函数Λm（ω）的脉冲响应函数λm（t）的有效宽度，选取相同的值。同样的，在实际应用中，首先在傅里叶空间内进行衰减模态修正，之后再通过傅里叶逆变换转换至时域空间，计算表达式如下：

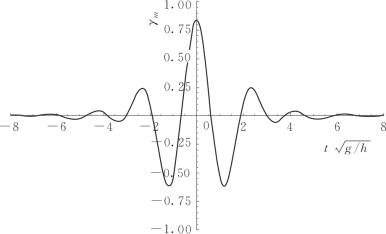
图5.5　衰减模态修正的脉冲响应函数γm（t）