生成斜向椭圆余弦波的方法

1.控制方程

式（2.10）给出了三维波浪生成的造波板运动位移X（y，z，t）的控制方程。由于长波的质点水平速度沿水深始终均匀，对于推板式造波机，造波板运动位移可简化为X（y，t）。图3.4所示为三维推板式分段造波机的示意图。由此，式（2.10）可重新写为

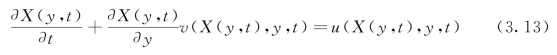
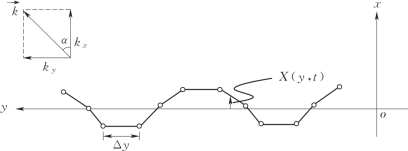
图3.4　三维推板式分段造波机示意图[6]

造波板处水质点的x方向和y方向速度分量根据连续性可通过式（3.14）得到。

初始条件为

周期性边界条件为

2.数值解

以下列波浪条件为例，介绍三维推板式造波机造波板运动位移的数值解求解过程。波浪波高H=0.20m，周期T=2.3s，水深h=0.4m，波向α=45°。在数值计算中，选取时间步长dt=T/300，空间步长dy=Ly/100。

（1）瞬态解。采用Mathematica软件，根据波面高程的表达式（3.11）直接求解偏微分方程式（3.15）～式（3.17），可以得到造波板运动位移的解，如图3.5和图3.6所示。从图3.5和图3.6中可见，造波板运动位移的解中存在一定的偏移，这是由于初始条件位移为“0”造成的。由于其非对称性，该解不适用于波浪物理模型试验中实际的波浪生成。因此，需要找到一种不存在偏移的、具有周期性的解，以符合造波板运动的实际情况且便于实验室中波浪生成的实施。将式（3.13）和式（3.14）合并，可以获得求解造波板运动位移X（y，t）的偏微分方程（PDE）：

图3.5　求解偏微分方程得到的造波板运动位移

（2）周期解。为了避免产生偏移的问题，通过一种假设将偏微分方程简化为常微分方程（ODE），之后利用求解常微分方程得到造波板运动位移的周期解。

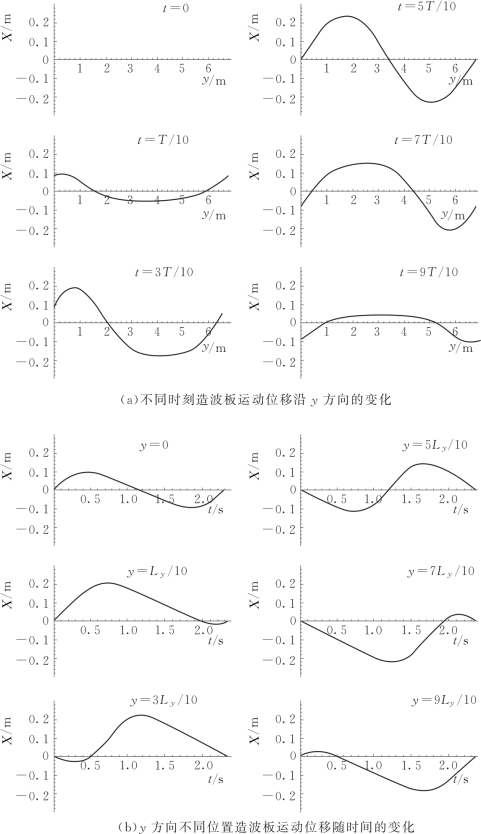
图3.6　造波板运动位移随时间和空间的变化

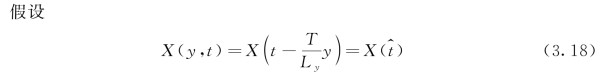
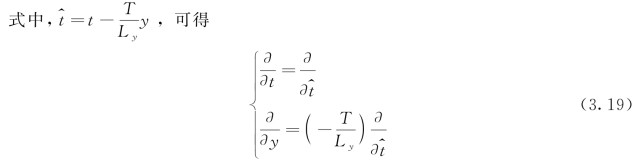(www.xing528.com)

由此，波面高程的表达式（3.11）可重新用式（3.20）表述

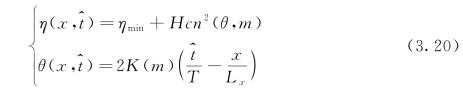
因此，偏微分方程式（3.15）可简化为如下形式的常微分方程：

利用有限差分法并根据波面高程表达式（3.20）和初始条件X（0）=0求解式（3.21），可以得到如图3.7所示的周期解X^（t）。

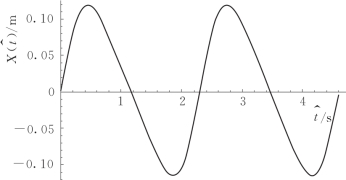
图3.7　造波板运动位移X^（t）随变量^t的变化过程

根据式（3.18）的假设，将造波板运动位移X^（t）转换为X（y，t）。图3.8显示了造波板位移X（y，t）随空间坐标y和时间t的变化情况。图3.8中可见，该周期解X（y，t）具有固定的形态，且沿坐标y和时间t均没有偏移。当t（或y）变化时，除相位不同以外，造波板位移随坐标y（或时间t）变化的形态相同。

（3）周期解的验证。偏微分方程的解存在偏移是由于静止的位移初始条件；常微分方程的解不存在偏移是利用了假设条件，且这种解符合实际的波浪生成情况。因此可尝试将常微分方程的解作为偏微分方程的初始条件来求解偏微分方程。求解过程利用显式有限差分法。针对项，在域内采用中心差分格式对其离散，左侧边界和右侧边界处分别采用前差和后差格式对其离散。式（3.15）在域内的离散形式可表示为

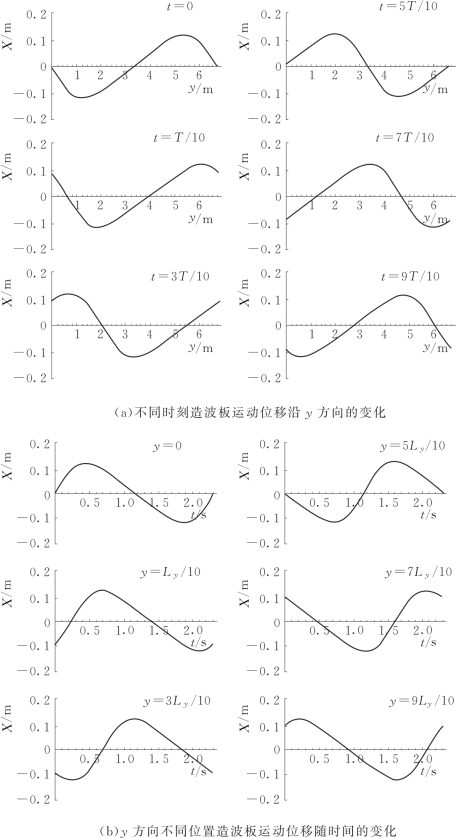
图3.8　造波板运动位移随时间和空间的变化

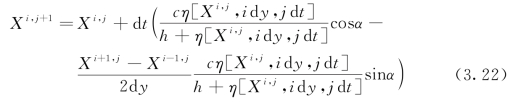
如图3.9所示为用常微分方程的解作为初始条件得到的偏微分方程的解。由图3.9中可见，蛇形解中不存在偏移。比较该偏微分方程的解与初始条件即常微分方程的解，相对误差的最大值为0.64%，表明常微分方程的解满足偏微分方程式（3.15），同时也证实了式（3.20）假设的合理性。因此，常微分方程的解适用于斜向椭圆余弦波的生成。

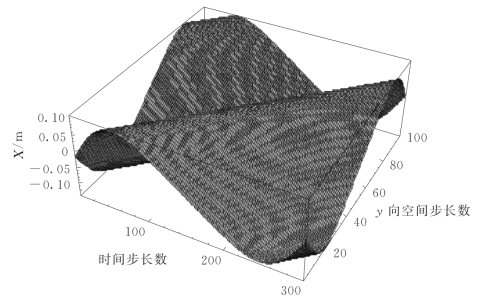
图3.9　常微分方程的解作为初始条件得到的偏微分方程的解（dt=T/300，dx=Ly/100）

参考文献

[1]Goring D.G.Tsunamis-the propagation of long waves onto a shelf[D].California:W.M.Keck laboratory of hydraulics and water resources，1979:9-45.

[2]Goring D.G.，Raichlen F.The generation of long waves in the laboratory[C].Proceedings of the 17th International Conference on Coastal Engineering，ASCE，Sydney，1980，1:763-783.

[3]Milne-Thomson L.M.Jacobian elliptic functions and theta functions，and elliptic integrals.In:Abramowitz M.and Stegun I.A.(Ed.)，Handbook of Mathematical Functions[M].New York:Dover Publications，1965.

[4]Svendsen I.A.，Jonsson I.G.Hydrodynamics of coastal regions[M].Lyngby:Den Private Ingeniørfond Technical University of Denmark，1980:163-178.

[5]Fenton J.D.Nonlinear wave theories.In:Le Mehaute B.&Hanes D.M (Ed.)，The Sea，Volume 9:Ocean Engineering Science[M].Cambridge，MA:Harvard University Press，1990:3-25.

[6]Schäffer H.A.，Steenberg C.M.Second-order wavemaker theory for multidirectional waves[J].Ocean Engineering，2003，30(10):1203-1231.