【摘要】：图3.1所示为椭圆余弦波基本参数定义图，设波高为H、周期为T的椭圆余弦波在水深为h的水域沿x方向传播，其波面高程η（x，t）的表达式为其中，cn（θ，m）为幅角θ和椭圆积分模数m的椭圆余弦。幅角θ为空间坐标x和时间t的综合参数，可由式（3.2）给出：图3.1椭圆余弦波基本参数定义图式（3.2）中，L为波浪传播方向x向的波长。椭圆余弦波的相速度可由式（3.5）计算得出。
波浪由深水向浅水区域传播时，由于水深变浅使波浪发生变形，外形变为不对称，波能量集中于尖突的波峰，且波峰大大高于静水位，而波谷平坦且离静水位较近。对形状不变的这种非线性波应用雅克比椭圆余弦函数[3]来描述波面高程时被定义为椭圆余弦波。文中椭圆余弦波理论的主要参考文献来自Svendsen和Jonsson（1980）出版的文献[4]及Fenton于1990年发表的文献[5]，与椭圆余弦波相关的椭圆函数简介参见附录B。
图3.1所示为椭圆余弦波基本参数定义图，设波高为H、周期为T的椭圆余弦波在水深为h的水域沿x方向传播，其波面高程η（x，t）的表达式为
其中，cn（θ，m）为幅角θ和椭圆积分模数m的椭圆余弦。幅角θ为空间坐标x和时间t的综合参数，可由式（3.2）给出：
图3.1 椭圆余弦波基本参数定义图
式（3.2）中，L为波浪传播方向x向的波长。
ηmin（＜0）为波谷高程，其表达式为
(www.xing528.com)
式（3.3）中，K（m）和E（m）分别为第一类和第二类椭圆积分。
椭圆积分模数m（0≤m＜1）为式（3.4）的解：
其中，Ur为Ursell数，它是体现波浪非线性特性
与色散特性
之比的一个重要参数。
椭圆余弦波的相速度可由式（3.5）计算得出。
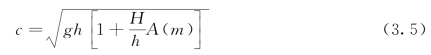
式中，相速度c定义为c=L/T。函数A（m）为
由此可得到波长L的表达式：
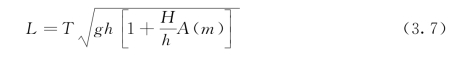
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
