复数形式的解详解

波浪物理模型域内的解可采用复数形式表达，具体表达式如下：

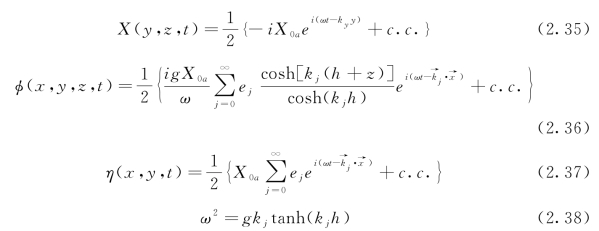
满足的条件为

式中：i为虚数单位；c.c.为前一项的共轭复数为复数形式的波数矢量（kxj，ky）；kj为波数矢量的长度为水平位移的矢量y）。

式（2.36）～式（2.38）中既包含了行进波又包含了衰减模态。k0为行进波的实数解，无限多个纯虚数kj为衰减模态的解，其中ikj=ksj＞0，（j=1，2，…）。

系数ej为复数形式的传递函数，定义如下：

其中，cj为对应于波浪传播方向，即ky=0的传递函数。对于推板式造波机可由式（2.41）计算得出。

可见除下标以外，式（2.41）与式（2.32a）相同。当j=0时，式（2.41）给出了行进波的实数传递函数c0，即Biesel传递函数[5]；而e0可以是实数，也可以是虚数，这取决于ky的选择。当j=1，2，…时，cj为虚数，式（2.32）中cj=-icsj，并且ej始终为虚数。

当时，kx为实数，生成的波浪场含有行进波的部分。行进波的波面高程可由下列形式表示：

其中，AI为复数形式的波幅，可由式（2.43）得到。

其中，e0为实数。当已知复数形式的造波板运动幅值Xa，即式（2.35）中Xa=-i X0a，可得

在这种情况下有如下关系式：

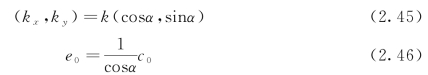
式（2.45）和式（2.46）中，对于j=0的行进波情况k和α的下标“0”被省略掉，α为行进波的波向，如图2.5所示。

图2.5　波数矢量的定义

当j=1，2，…时，式（2.36）～式（2.38）中kxj为虚数，它对应于衰减模态。复数形式的αj定义如下：

(www.xing528.com)

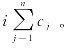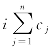针对推板式造波机，图2.6给出了Biesel传递函数c0和不同衰减模数n条件下总的衰减模态传递函数由图2.6可知，当无量纲化的频率时，Biesel传递函数c0达到其极值2；衰减模态传递函数随着频率的增加而逐渐增大。另外对于衰减模态，当衰减模数n逐渐增大时，传递函数也随之增大且逐渐接近于渐进曲线。当时，衰减模数n=20与n=200条件下几乎不变。此外，当ωh/g增加到某一值以后大于c0。例如，当时这就意味着频率越高，衰减模态的影响越大。当频率增大到一定程度时，衰减模态引起的造波板处局部扰动的幅值超过行进波的幅值。这也说明了推板式造波机对生成高频波存在的问题。

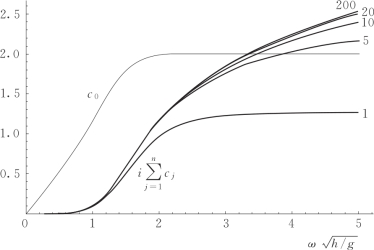
图2.6　推板式造波机情况下传递函数c0及不同n条件下总的衰减模态传递函数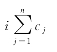

图2.7给出了推板式造波机情况下传递函数e0和几种不同波浪传播方向条件下总的衰减模态传递函数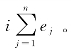在此及后续衰减模态中取衰减模数n=20。从图2.7中可见，当波向α增大时，传递函数e0随之增大，但衰减模态传递函数随之减小。

当时，即使在j=0条件下仍然为衰减模态，而不能产生行进波。

图2.7　推板式造波机情况下传递函数e0及不同波向下总的衰减模态传递函数

针对行进波，沿水深平均的水平速度U（x，y，t）可定义为

式中u（x，y，t）可通过式（2.36）中行进波部分的速度势计算得出。

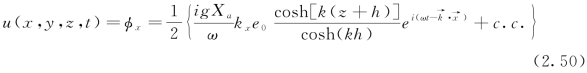
利用色散关系可得

将式（2.51）代入式（2.49）可得

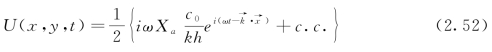
令BI表示U（x，y，t）的复数形式的幅值，由此可得

参考文献

[1]Dean R.，Dalrymple R.A.Water Wave Mechanics for Engineers and Scientists[M].Singapore:World Scientific，1984.

[2]Schäffer H.A.，Steenberg C.M.Second-order wavemaker theory for multidirectional waves[J].Ocean Engineering，2003，30(10):1203-1231.

[3]Madsen O.S.A three-dimensional wavemaker，its theory and application[J].Journal of Hydralulics Research，1974，12(2):205-222.

[4]Schäffer H.A.Second-order wavemaker theory for irregular wave[J].Ocean Engineering，1996，23(1):47-88.

[5]Biesel F.，Suquet F.Les Appareils Generateurs de houle en laboratoire[J].La houille blanche，1951，6:152-165.