单相正弦交流电路鉴定点15

问：如何分析和计算单相正弦交流电路？

答：分析和计算单相正弦交流电路的方法如下：

（1）纯电路的分析与计算 纯电路是指纯电阻、纯电感和纯电容电路。

1）纯电阻正弦交流电路。交流电路中如果只有线性电阻，这种电路就称为纯电阻电路。

在纯电阻正弦交流电路中：

①电压与电流同相位，即电压与电流的相位差φ=0。

②电压与电流有效值关系为

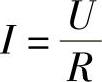
③电路的功率 电压瞬时值u和电流瞬时值i的乘积称为瞬时功率，用p表示，即

p=ui

平均功率是指瞬时功率在一个周期内的平均值，平均功率又称为有功功率，用P表示，即

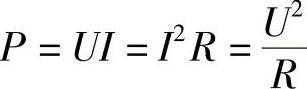
2）纯电感正弦交流电路。在交流电路中，如果只用电感线圈作负载，而且线圈的电阻和分布电容均可忽略不计，这样的电路就叫做纯电感电路。

①纯电感电路中，电感两端的电压超前电流90°，设i=I_msinωt，则

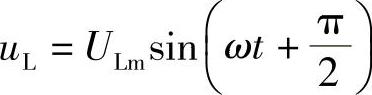
②电流与电压的最大值及有效值之间也符合欧姆定律，即

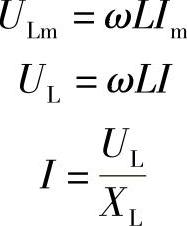
X_L称为感抗，表明电感具有阻碍交流电流流过电感线圈的性质。感抗X_L等于电感元件上电压与电流的最大值或有效值之比，不等于它们的瞬时值之比。

感抗的计算公式为X_L=ωL=2πfL

感抗的单位为Ω。

③纯电感电路的功率。

a.瞬时功率等于电流瞬时值与电压瞬时值的乘积。

b.平均功率等于零，即P=0，也就是说电感元件在交流电路中不消耗电能。

c.无功功率。电感线圈不消耗电源的能量，但在电感元件与电源之间不断地进行周期性的能量交换。为了反映电感元件与电源之间进行能量交换的规模，把瞬时功率的最大值叫做电感元件上的无功功率，用符号Q_L表示，其表达式为

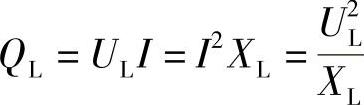
无功功率的单位为var和kvar。

注意：“无功”的含意是“交换”而不是消耗，是相对“有功”而言的，绝不能理解为“无用”。

3）纯电容正弦交流电路。在交流电路中，如果只用电容器作负载，而且电容器的绝缘电阻很大，介质损耗和分布电感均可忽略不计，这样的电路称为纯电容电路。

在纯电容电路中：

①电流在相位上超前电压90°。

②电流与电压的最大值及有效值之间也符合欧姆定律。

③X_C起着阻碍电流通过电容器的作用，所以把X_C称为电容器的电抗，简称容抗。其计算式为

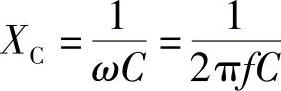
容抗的单位为Ω。容抗X_C等于电容元件上电压与电流的最大值或有效值之比，不等于它们的瞬时值之比。

④纯电容电路的功率。

a.纯电容电路的瞬时功率同样可用p=ui求出。(www.xing528.com)

b.平均功率为零，即电容器不消耗能量。

c.无功功率等于瞬时功率的最大值，用Q_C表示，即

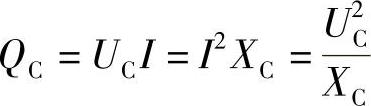
无功功率的单位为var和kvar。（2）RLC串联电路 电阻、电感和电容的串联电路称为RLC串联电路。设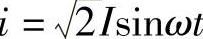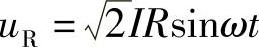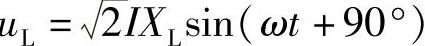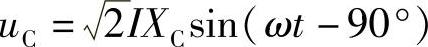，，，，则电路的总电压为

u=u_R+u_L+u_C对应的相量关系为U=U_R+U_L+U_C。在RLC串联电路中：1）电压与电流的相位关系为

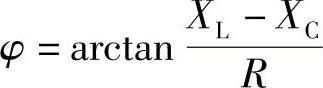
①X_L＞X_C时，总电压超前电流，电路呈感性。

②X_L＜X_C时，总电压滞后电流，电路呈容性。

③X_L=X_C时，总电压与电流同相位，电路发生串联谐振，电路呈阻性，如图1-10所示。

2）总电压与总电流、总电压与各分电压之间的关系为

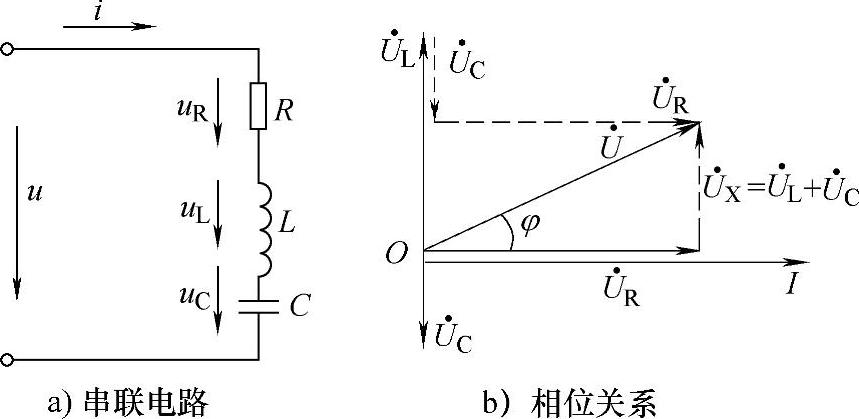
图1-10 RLC串联电路电压与电流的相位关系

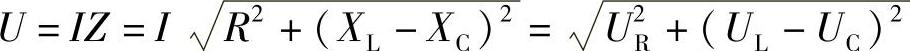
总电压与分电压组成电压三角形，如图1-11所示。

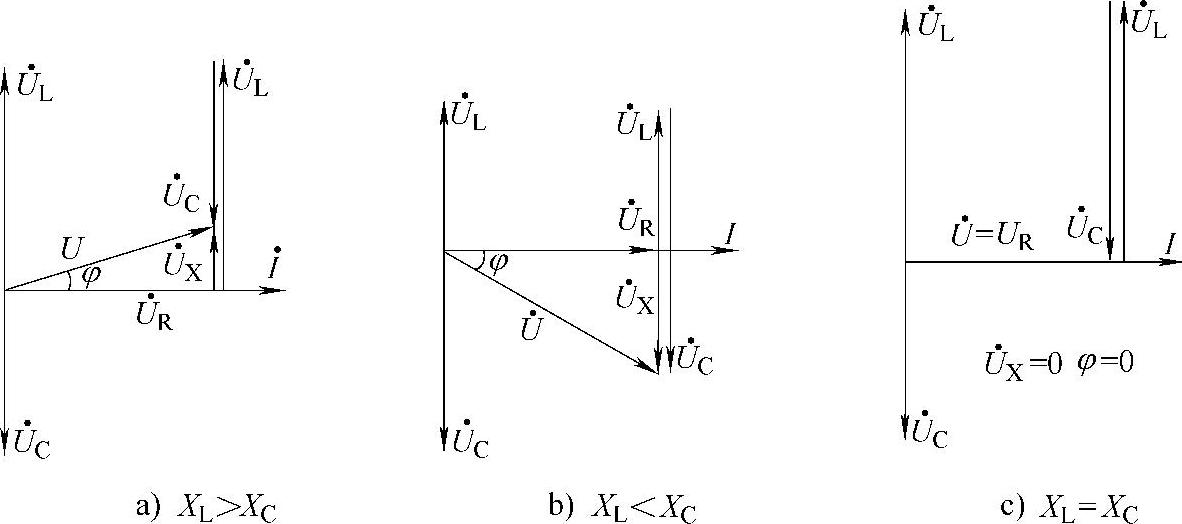
图1-11 RLC串联电路总电压与总电流、总电压与各分电压之间的关系

3）总阻抗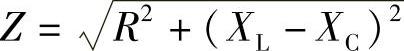，其中X_L-X_C称为电抗。Z、R、X组成阻抗三角形，阻抗角为φ=arctan（X_L-X_C）/R

4）电路中的功率。

①有功功率。电阻消耗的功率为总电路的有功功率，即

P=I²R=UIcosφ

有功功率的单位为W。

②无功功率。总的无功功率等于电感和电容上的无功功率之差，即

Q=Q_L-Q_C

无功功率的单位为var和kvar。

当X_L＞X_C时，Q为正，表示电路中为感性无功功率；当X_L＜X_C时，Q为负，表示电路中为容性无功功率；当X_L=X_C时，无功功率Q=0，电路处于谐振状态，只有电感与电容之间进行能量交换。

③视在功率。电路的总电压与总电流有效值的乘积称为电路的视在功率，用S表示，即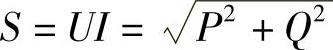

视在功率的单位为V·A和kV·A。

有功功率为P=Scosφ

无功功率为Q=Ssinφ

视在功率、有功功率和无功功率组成功率三角形，如图1-12所示。

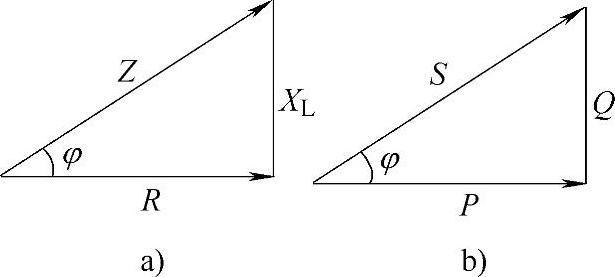
图1-12 功率三角形

【试题精选】在RL串联正弦电路中，电阻上的电压为6V，电感上的电压为8V，则总电压为（CC）V。

（A）14（B）2（C）10（D）48