线性系统与控制概述

A.2.1 状态变量和状态方程

一个动态系统的“状态变量”是“最少”的一套变量，通常表示成x₁（t），x₂（t），…，x_n（t）。可以用n个一阶线性微分方程来完全描述系统的动态行为：

式中u_i（t），i=1，2，…，m代表系统的（控制）“输入”，系数a和b都是（不随时间变化的）常数。这些一阶线性微分方程就被称为动态系统的“状态方程”。

系统的“输出”，通常表示为y（t），是指那些测量的变量（使用传感器）。如果它们线性地依赖于系统的状态变量和输入，那么它们可以通过数学方程描述为：

式中p≤n，系数c和d都是常数。式（A-1）和式（A-2）可以写成更为简洁的向量矩阵形式

式中、x（t）、u（t）和y（t）分别是状态导数、状态变量、输入和输出的n×1、n×1、m×1和p×1向量。而A、B、C和D分别是n×n、n×m、p×n和p×m矩阵。

例：用状态方程描述一个质量-弹簧-阻尼系统。

首先要注意，一个质量-弹簧-阻尼系统的动态行为可以由二阶线性微分方程来完全描述：

如图A-1所示，其中y（t）代表质量M在力u（t）下的位移，B和K分别是系统的阻尼和弹簧常数。

让我们把两个新的变量x₁（t）=y（t）和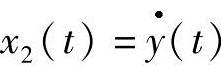定义成系统的状态变量。然后，经过一些简单的代数，可以把式（A-4）改写成等同的一阶线性微分方程组，来代表质量-弹簧-阻尼系统的二阶状态方程描述：

这也可以表示成向量矩阵形式

图A-1 质量-弹簧-阻尼系统

A.2.2 非线性系统的线性近似

一个非线性动态系统可以定义状态变量，用来得到状态方程组。尽管这些方程是非线性的，但它可以描述这个系统的动态性能。然而，假设系统在有限的范围内工作，例如，在一组状态变量和输入值（x₀，u₀）定义的工作点或平衡点附近，变量改变不多，我们可以在这个范围内把系统的性能（用电子工程术语称为小信号性能）近似成一组“线性”状态方程。在许多像文献[1]这样的本科控制系统教科书中，我们可以找到这样做的泰勒级数展开标准步骤。在3.5.1节中，我们已经用同样的近似方法得到质子交换膜燃料电池的线性模型。

例如一个普通二阶非线性系统的线性近似：

假设有一个二阶动态系统，它的状态变量是x₁、x₂，并且只有一个输入u，系统可以由非线性状态方程来描述：

其中f₁和f₂是非线性函数。如果系统的工作点值是（x₁₀，x₂₀，u₀），那么式（A-7）的线性近似是

请注意，在工作点值计算偏导数，会给出式（A-8）中的常系数x₁，x₂，和u。A.2.3 线性系统的特征方程、特征根和特征值

对于线性状态方程[式（A-3）]所描述的动态系统，它的输入、输出“传递函数”可以表示为

式中s是拉普拉斯变换的复数频率变量，I是单位矩阵。此外，系统的“特征根”是sI-A等于0时的矩阵行列式根（s的n阶多项式）

|sI-A|=0 （A-10）(www.xing528.com)

这些n个根也是系统的“极点”（受系统零的精确取消影响），换个方法，我们可以通过寻找系统矩阵A的“特征值”得到。A.2.4 线性状态反馈控制

我们考虑一个状态方程[式（A-3）]描述的线性动态系统，它的控制有以下形式

u（t）=-Kx（t） （A-11）

式中状态反馈增益K是一个有常数元素的向量（或在多输入情况下的矩阵）。这种形式的控制意味着：

1）所有的状态变量是可测量的，而且也被测量了；

2）控制是状态变量的一个线性组合；

3）包括方程式（A-3）和式（A-11）的闭环控制系统现在可以描述成

4）这个闭环系统的特征方程给出如下

|sI-（A-BK）|=0

现在，如果矩阵对（A、B）能使开环系统[式（A-3）]成为完全状态控制的^[1]，那么通过适当选择元素K，闭环系统的特征根可以被“放置”在复数s-平面的任何地方（只要复根是共轭对）。这种状态反馈增益的设计步骤通常称为“极点配置”设计。

例如一个普通二阶系统的状态反馈极点设置：

假设我们有一个由状态方程描述的动态系统

这个系统的特征方程给出如下：

s²+a₁s+a₀=0 （A-14）

有两个特征值（极点）可能在不需要的位置上，例如，在右半s-平面，对应于一个不稳定的系统。因为（A、B）是这个系统的完全可控矩阵对，所以可以使用状态反馈控制，把闭环系统的极点放置在任何其他位置上。然而我们必须使测量的输出

y（t）=x（t）

然后，K=（k₀k₁）给出需要的状态反馈增益，这意味着，在状态反馈控制下的系统可以描述成

这就得出了特征方程

s²+（a₁+k₁）s+（a₀+k₀）=0 （A-16）因此，可以适当选择K元素来得到所需的特征方程。这对应着闭环系统的极点放置在能产生预期系统稳定性和性能特点的位置上。