配电系统负载流量分析

现在已经有成熟的电力传输系统负载流量分析方法。典型的方法包括Gauss-Seidel法、Newton-Raphson法和快速解耦法。所有这些方法可以直接应用于配电系统。而且针对配电系统自身放射结构的特点，已经提出了一些新方法。

配电系统已经有四种典型的流量分析方法：Gauss-Seidel法、Newton-Raphson法、DistFlow法和精确法。在本节中，我们将简要介绍其中三种方法。

1.Gauss-Seidel法

对于传输网络，Gauss-Seidel算法基本是迭代数值法，优点是过程简单，可以直接用于配电系统。Gauss-Seidel算法，反复尝试寻找系统线性方程组的解，直到迭代的解是在预定可接受误差范围内。这是个强大可靠的负载流量方法，即使面对极为复杂的电源系统都是收敛的。Gauss-Seidel算法的迭代过程，给出如下：

式中 V_k（i+1）和V_k（i）——第i+1次和第i次迭代的总线k电压值；

P_k和Q_k——总线k注入的有功功率和无功功率；

Y_kk和Y_kn——阻抗矩阵元素。

2.Newton-Raphson法

Guass-Seidel法的缺点是每条总线都是独立处理的，即每条总线在修正后，需要修正所有与它相连的总线。然而，Newton-Raphson法是根据同时考虑所有相互作用来计算修正的。

为了解非线性方程f（x）=b，我们用牛顿法来调整与函数独立变量的Δx，使函数的误差趋向零。函数f（x）对于某个特定x⁰的泰勒展开是

设定误差ε为零，我们得到

上述方程是每个迭代调整的计算式。

把上述想法运用到电力系统中，就可以进行功率流分析的Newton-Raphson法推导。

对于每个总线i，有以下功率平衡方程：

P_i+jQ_i=V_iI_i^* （8-34）

式中 P_i+jQ_i——总线i的复功率；

V_i和I_i——总线i的电压和注入电流相量。

变量是电压大小V_i和电压角θ_i。因此，我们需要把功率平衡方程写成：

对上述方程求导，并考虑这个方程的实部和虚部，我们得到：

根据式（8-36），可以得到迭代的调整计算：(www.xing528.com)

ΔX=[J]^-1ΔZ （8-37）

式中

关于Newton-Raphson法功率流分析的详细资料，读者可参考有关电力系统分析或计算的任何书籍。

3.DistFlow法

这个方法是由MesutE.Baran和FelixF.Wu开发的，目的是解决电容器的优化布局。

根据放射状分配系统的结构特性，放射状分配系统的功率流方程也称为Dist-Flow方程，包括分支流方程和与每个横向相关的边界条件，其中包含被看做是零横向的主馈线。它们的形式如下：

式中X=[x_i^T…x_l^Tx₀^T]^T

x_k=[x_k0^T…x_kn^T]^T

对于一个包括主馈线和m个主横向的放射分布分配系统，我们需要解以下2（m+1）个方程：

或者向量形式的方程：

H（Z）=0 （8-41）

式中，Z=？Z₁₀^T…Z₁₀^TZ₀₀^T」是状态变量向量。

用Newton-Raphson法可以解这个负载流量问题：

步骤1：对于估计给出的Z⁰，计算H（Z⁰）的不匹配。

步骤2：生成雅可比矩阵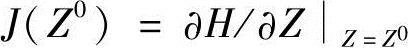

步骤3：解下面的方程系统，来更新状态Z：

J（Z⁰）ΔZ⁰=-H（Z⁰）

DistFlow法的细节详见文献[36，37]。