质子交换膜燃料电池的子系统介绍

这里的描述是为了完整性。文献[17]中的质子交换膜燃料电池模型开始于Nernst方程定义的理想势能，这是Larminie和Dicks在文献[25]中介绍的。理想势能把反应物和产物浓度与在平衡条件下电化学反应产生的电位差联系起来。然后我们用美国能源部2001年未来能源挑战学生设计竞赛的燃料电池模型^[19，20]来构造电池的电压方程

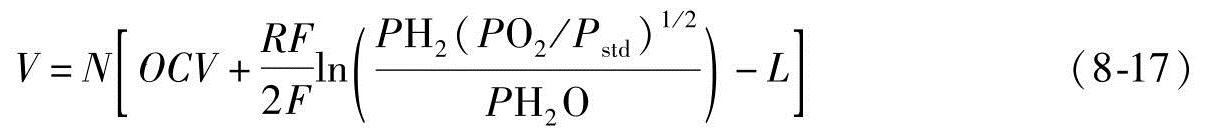
这是我们已经在前面第3章介绍的。

燃料电池的实际电压可以用以上定义的理想势能^[25]减去不可逆损失L来推导。这些不可逆损失主要有四类：激活损失、欧姆损失、浓度损失和内部电流损失。像第3章讨论的，电压损失L可以描述为

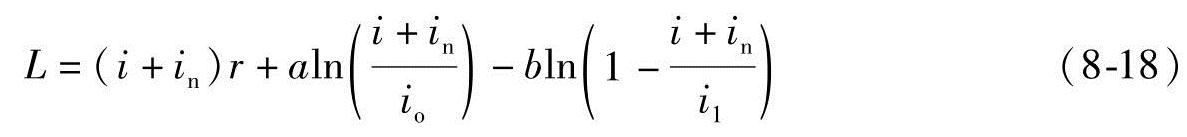
我们定义氢气、氧气和水的分压为三个系统状态变量。此外，由于水管理影响燃料电池的性能，我们在阳极和阴极两侧使用加湿器来控制电池内的湿度。考虑阴极侧的水比考虑阳极侧的水更为复杂，因为它不仅包括加湿器提供的水，而且包括反应副产物的水。

图8-2演示了这些气体是如何流入和流出电池的。

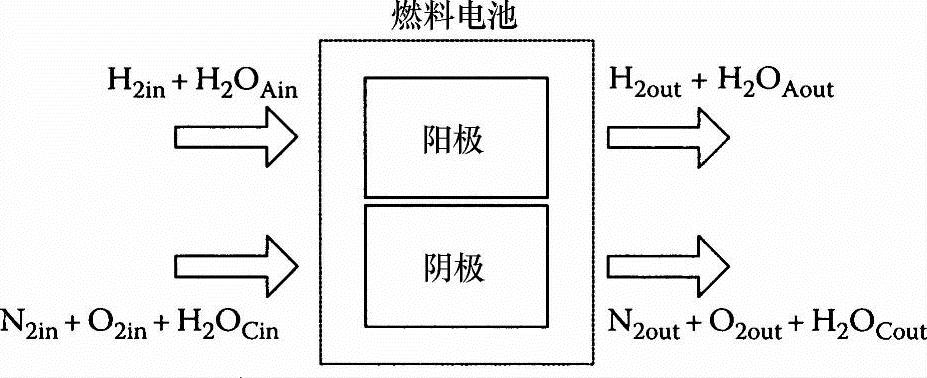
图8-2 质子交换膜燃料电池的气体流动示意图

根据理想气体定律PV=nRT，每种气体的分压与电池内的气体量成正比，后者等于入口气流量减去耗气量和出口气流量。因此，状态方程是

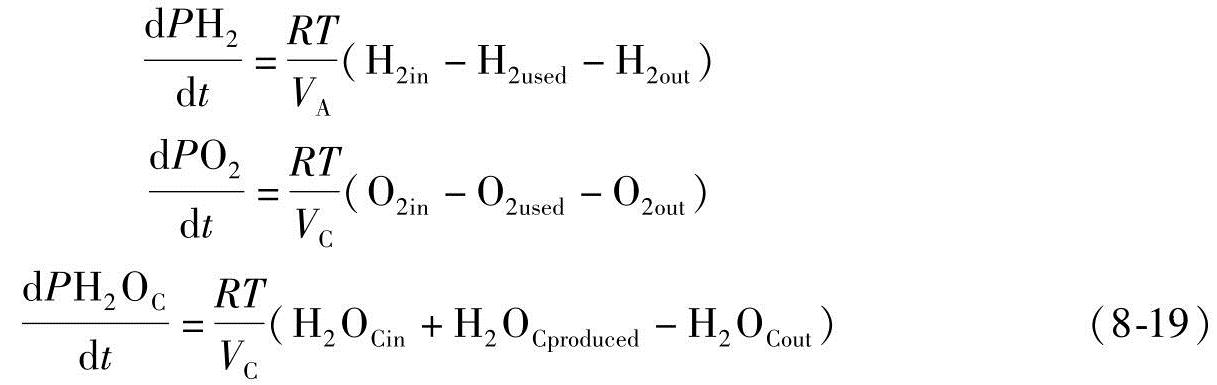
式中 H_2in、O_2in和H₂O_Cin——阴极侧入口氢气、氧气和水的流率；

H_2out、O_2out和H₂O_Cout——氢气、氧气和水的出口流率；H_2used、O_2used和H₂O_Cproduced——氢气、氧气和水的使用率和产生率，它们与输出电流I的关系是

H_2used=2O_2used=H₂O_Cproduced=2K_rI=2K_rA_ci （8-20）(www.xing528.com)

式中 K_r=N/4F（mol/C）；

A_c——电池有效面积（cm²）；

i——电流密度（A/cm²）。

由于入口流率和输出电流是可测量的，出口流率可以由以下方程定义：

H_2out=（Anode_in-2K_rA_ci）FH₂

O_2out=（Cathode_in-K_rA_ci）FO₂

H₂O_Cout=（Cathode_in+2K_rA_ci）FH₂O_C （8-21）

式中，Anode_in和Cathode_in分别是图8-2所定义的阳极入口流率总和及阴极入口流率总和。FH₂、FO₂和FH₂O_C分别是燃料电池内每种气体的压力分数。

在美国能源部模型中

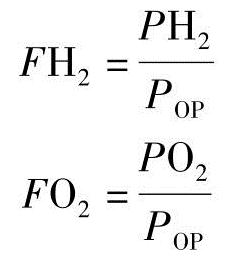
其中假设电池的压力保持在恒定值P_op，也就是稳态工作压力101kPa。