如何在Simulink中建立燃料电池模型？

为了在Simulink中创建一个燃料电池的模型，我们做以下假设：

●由于电池堆温度的响应时间很慢（约102s^[1]），假设电池堆的工作温度是恒定的。

●在燃料电池阳极和阴极两侧都被很好地加湿。

●对水的管理，假设液态水不离开电池堆，如果阴极或阳极任何一侧气体湿度降至低于100%，液态水会蒸发补充^[2]。

●假设加湿器和温度控制器工作完美^[3]。

●为了建立燃料电池的简化动态模型（图5-1），假设入口反应物的摩尔分数为常数。换句话说，纯氢气（99.99%）被直接输入阳极，空气（按着氮和氧21∶79的比例均匀混合）被送入阴极^[3]。

●假设所有气体都是理想气体，可以使用理想气体定律和摩尔守恒定律。

因此，在这个模拟中，水管理和温度控制不是问题。燃料电池系统包括四个部分：阳极模型、阴极模型、燃料电池电压模型和控制模块。

首先考虑燃料电池电压模块。燃料电池堆输出电压V_st被定义为以下参数的函数：电池堆电流、反应物分压、燃料电池温度和膜湿度。

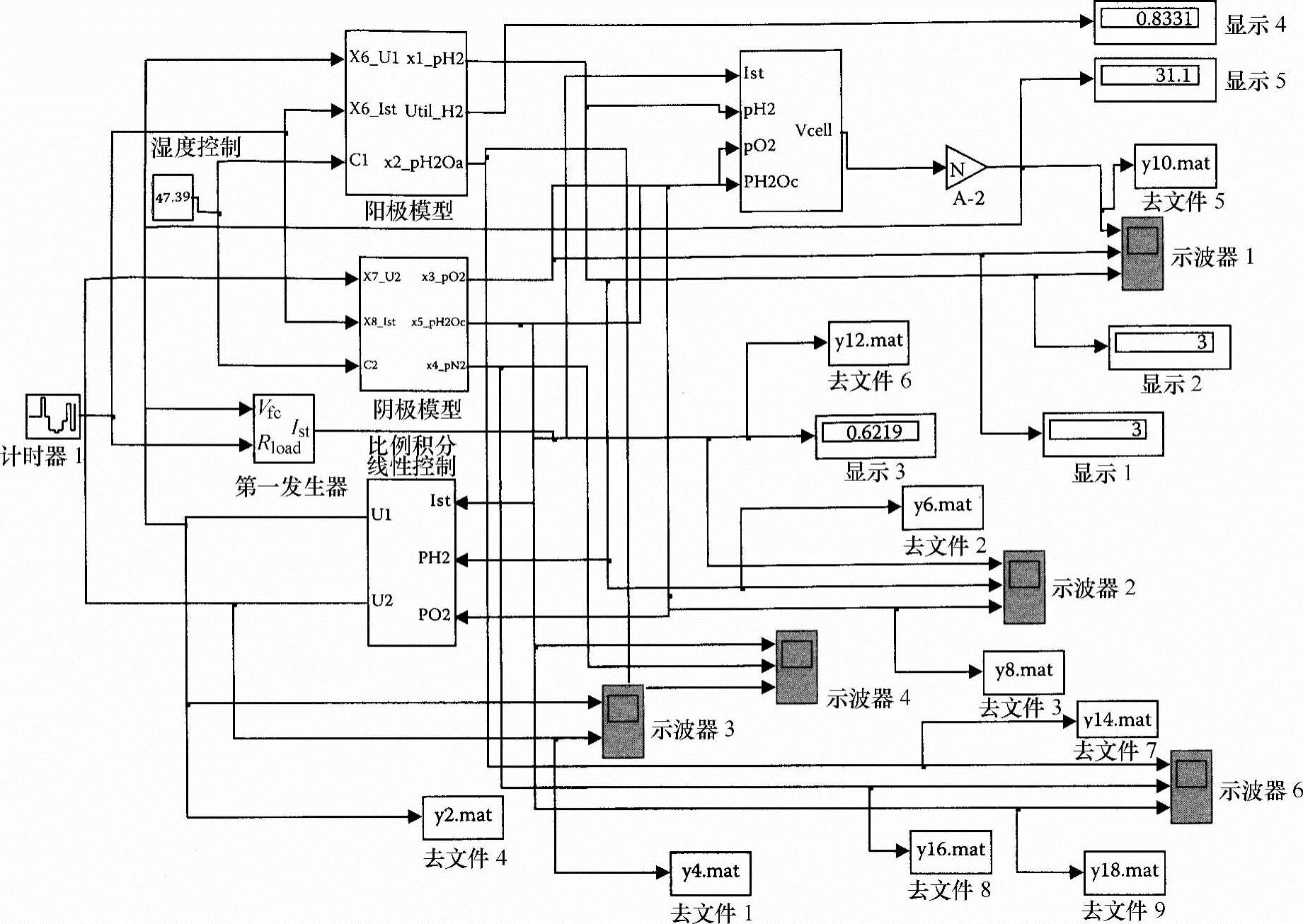
图5-1 质子交换膜燃料电池的系统框图

V_st=E-V_activation-V_ohmic-V_{concentration}（5-1）

式中

——电池的热动力学势能或Nernst方程中的可逆变电压[式（5-1）]；

V_activation——电极表面反应速率导致的电压损失；

V_ohmic——电解质中质子流电阻导致的电压损失；

V_{concentration}——因浓度降低或氧气和氢气质量输送导致的电压损失。

它们的值给出如下：

V_ohm=N·I_fc·r （5-3）

V_concentraion=N·mexp（n·Ifc） （5-4）

在式（5-1）的E中，，和分别是氢气、氧气和水的分压；下标“c”代表从阴极侧排出的水的分压。

在文献[2]中，详细解释了每个电压损失。在文献[1，3]中介绍了其他电压，其中的燃料电池电压主要表达为一些参数的物理和经验关系的组合，这些参数包括膜含水量、湿度、温度及反应物浓度（表5-1）。在本书中，我们将使用式（5-1）给出的普遍电压公式。因为水和温度的响应时间很慢，我们假定它们是恒定的。图5-2是根据式（5-1）设定的燃料电池电压模块。

表5-1　电池电压参数(www.xing528.com)

出自：Khan，M.J.and Labal，M.T.，FuelCells，4，463，2005.许可使用。

阳极和阴极侧的反应物流率是由分压和电池堆电流决定的。如图5-3所示，使用理想气体定律，我们可以模拟每个分压模块。从图5-3中可以看到，阳极模块包括氢气模型和水模型。每个压力的输出，甚至是控制器的输出，都有限制器，这是为了防止代数循环或极端数值造成问题^[1]。图5-4和图5-5分别是详细的氢气模型和水模型。

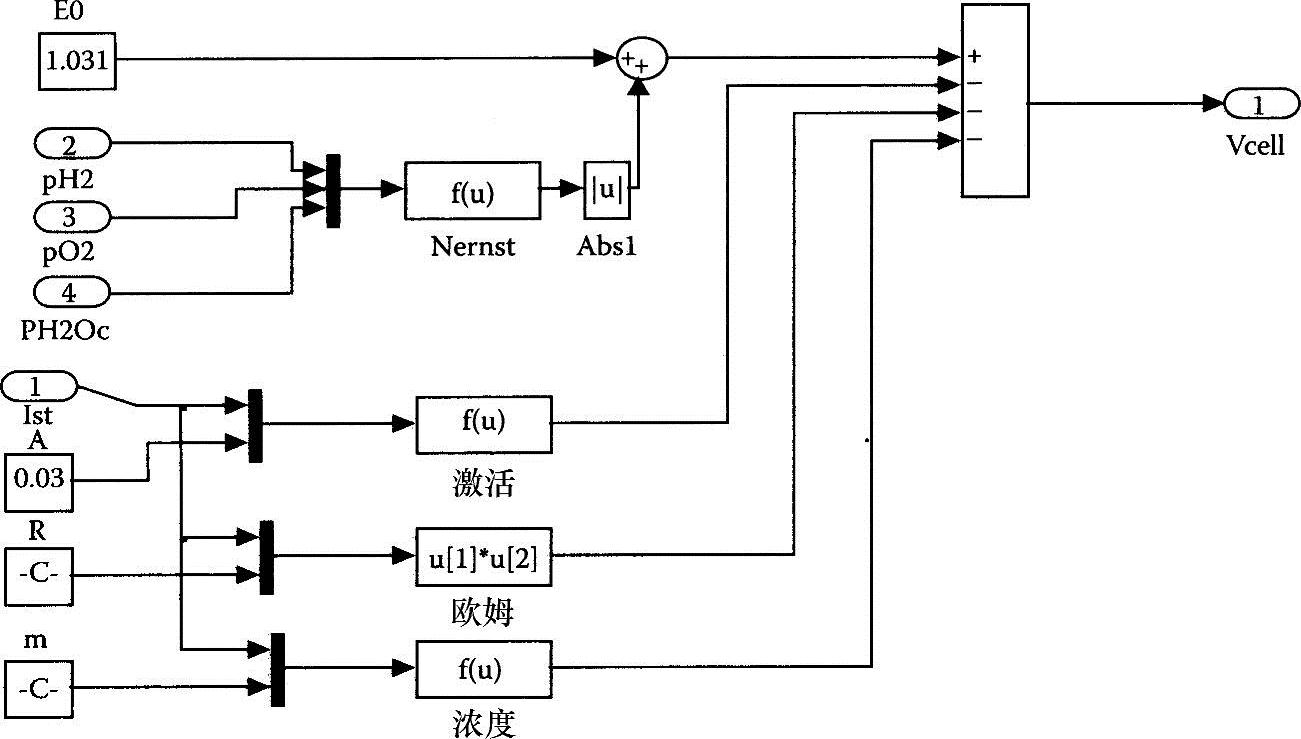
图5-2 燃料电池电压模块

图5-3 阳极模块

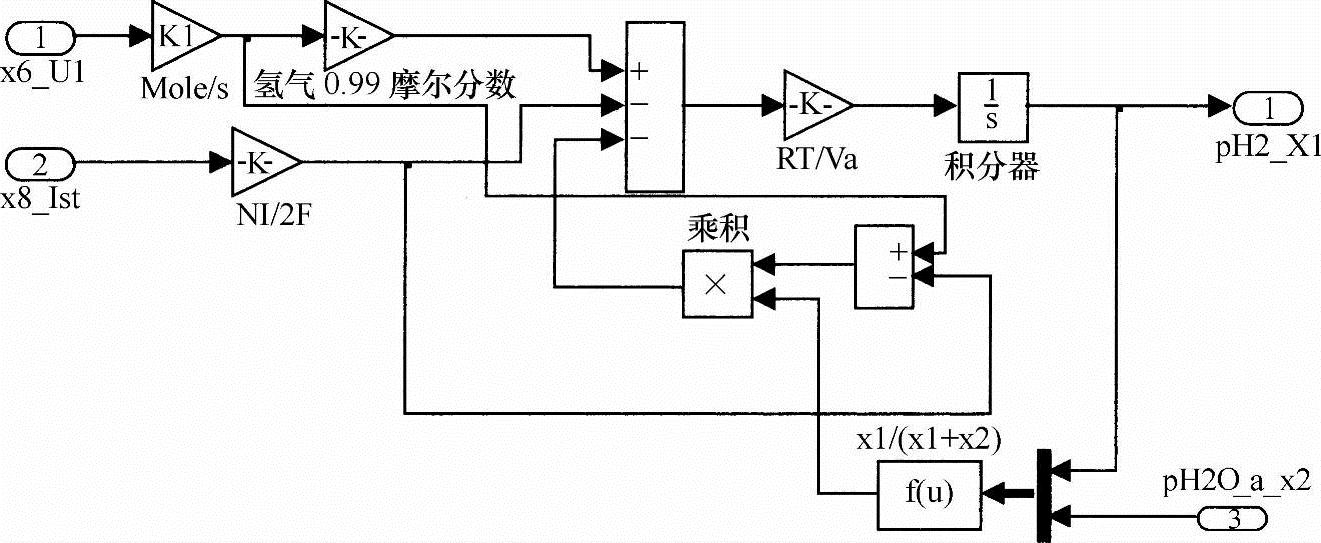
图5-4 氢气模型

图5-5 阳极侧水的模型

阴极模型包括图5-6～图5-9所示的氧气，水和氮气模型。

图5-6 阴极模型

在阳极模块中，假设氢气的摩尔分数是99%，我们用一个转换因子把氢气入口流率从L/min转换成mol/s（每分钟一标准升为7.034×10^-4mol/s）。在阴极模块中，空气是按氮气和氧气21∶79的比例均匀混合的，转换因子是7.034×10^-4 mol/s^[1]。为了在很短的时间内分析数据，我们使用了一个快速常微分方程求解程序Ode45，该程序基于Dormant-Prince算法，是直接的一步Runge-Kutta数值法。我们推荐拿它作为第一个尝试的方法^[4]。尽管它的设置时间是100s，但是可以在10s内得到并显示所有的模拟结果。我们可以看到，在0～0.5s之间，模拟结果有一些不现实的值，这是由于初始条件不足造成的。

图5-7 氧气模型

图5-8 氮气模型

图5-9 阴极侧水的模型

电池堆电流是由电池电压V_fc和负载模块R_load生成的。负载模块是由计时器制成的，它的时间矩阵是[0，15.0，20.0，25.0，30.0，35.0，40.0，45.0，50，55s]，对应于振幅电阻矩阵[1，0.6，0.3，0.175，0.3，1，2.5，5，1，5Ω]。