燃料电池非线性控制的优化设计

在本节我们会推导燃料电池的多输入输出非线性动态模型，然后用反馈线性化设计非线性控制器，来减少氢气和氧气之间的分压差ΔP。保持ΔP在一定小的范围内，主要是为了保护膜不受损伤，从而延长燃料电池堆的寿命^[4，5]。此外，压力比其他参数对燃料电池性能的影响更大^[4，5]。因为燃料电池的电压是压力的函数，所以我们需要适当地控制每个压力，以避免有害的燃料电池电压降。为了达到这一目的，我们必须使用精确阀控制器这样的精确执行器来尽量减少阳极和阴极之间的压力差。在通常情况下，最优压力控制器由压力传感器和电磁流率控制阀组成。在这本书中，我们主要是为整个燃料电池系统设计压力控制算法，而不是设计燃料电池内部的压力传感器和流率控制器。此外，因为电压-电流极化曲线的特性使很短时间内的电压控制难以执行，所以我们不把燃料电池的电压当成控制输出。通常燃料电池系统需要辅助的能源储存装置来实现短时间内的电压控制。因此，我们只选择氢气和氧气分压作为控制输出，而把电池堆电流看做对系统的干扰，而不是外部输入^[5]。

考虑下面有小波动的多输入输出非线性系统：

式中 x⊂Rⁿ——状态向量；

[u₁，u₂，…，u_m]=U⊂R^m——输入或控制向量；

y⊂R^P——输出向量；

f（x）和g（x），i=1，2，…，m——n维光滑向量场；

d——小波动变量；

p（x）——与小波动直接相关的空间向量场。

考虑下面有小波动的多输入输出非线性系统，燃料电池的非线性动态系统模型可以改写如下：

式中

f（x）=0；

式（4-2）暗示了系统的输入输出性能是非线性的和耦合的。我们必须采取两个步骤才能达到控制目的：

●不仅可以得到补偿非线性，而且可以得到把输入和输出性能去耦并线性化的非线性控制律。

●在闭路中放入奇异点，当加入比例积分控制器后，可以使输出P_H2和P_O2按期望的轨迹渐近跟踪。

式（4-2）提供了一个多输入输出非线性系统，使我们可以求出非线性控制律。在通常情况下，不能在控制设计中直接使用式（4-2）中的小波动d，因为必须先满足额外的必要条件，即能够测量干扰而且不允许有前馈作用^[6，7]。否则，新输入v和输出y之间的线性映射不存在。使用干扰的测量，这个条件给出下面的控制律：(www.xing528.com)

U=-A^-1（x）b（x）+A^-1（x）v-A^-1（x）p（x）d （4-3）

如式（4-2）所示，f（x）=0导致b（x）=L_f^rh（x）=0，所以控制律可以写成

U=A^-1（x）v-A^-1（x）p（x）d （4-4）

由于在对每个y₁=x₁和y₂=x₃求一阶导数后，每个控制变量u才显露出来，相对度向量[r₁r₂]是[1 1]，而去耦矩阵A（x）被定义为

式中

在x=x₀点非奇异。此外，式（4-4）中的矩阵v和p（x）给出如下：

式（4-4）给出的控制律使输入输出性能去耦并线性化（见图4-1）：

输出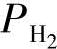和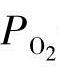按照新输入v₁和v₂是去耦的。因此，在输入v₁和氢分压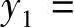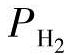之间，在输入v₂和氧分压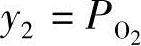之间，可以得到两个线性子系统。此外，注意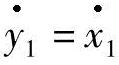和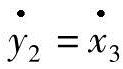，所以为了确保y₁和y₂被调整成y₁s和y₂s的期望值3atm（1atm=0.1MPa），我们要用线性控制理论的极点配置方案来设计稳定控制器[8]。新的控制输入给出如下

式中e₁=y₁-y_{1_s}而且e₂=y₂-y_{2_s}。

尽管可以通过反馈线性化把非线性燃料电池系统精确线性化，但是在参数变化中，特别是当负载变化时，有可能存在跟踪误差。如文献[7，8]所示，为了消除这种跟踪误差，我们在闭环误差方程中加入了积分项：

从式（4-9），可以得到如下误差动态性能：

适当选择s²+k₁₁s+k₁₂和s²+k₂₁s+k₂₂的特征根，可以实现渐进跟踪，所以当t→∞时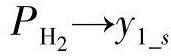，，而且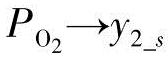。选择k²₁₁＞＞4k₁₂和k²₂₁＞＞4k₂₂也可以减少过冲。

如图4-12所示，这个控制方案的主要目是通过适当定义一个变换映射来设计非线性控制器。这个映射可以把原来的非线性系统变换成线性可控（封闭）系统，再使用极点配置技术达到跟踪目的，然后就可以设计线性控制器。然而，我们将无法观察到式（4-4）中的控制律，因为整个动态有五个元素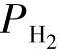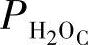（，…，），而只有两个元素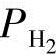（和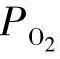）在输出中可以观察到。因此，它可能有内部动态的问题。换句话说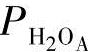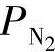，、和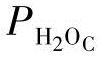的内部动态必须是稳定的，这样在跟踪时，式（4-9）中跟踪控制器的状态才能被限制在有界区域内。否则，因为外部和内部动态，这种控制法不能提高整体系统性能。然而，很难直接确定系统的内部动态，因为它是非线性的、非自治的，并且耦合到外部闭环动态中，这也可以从式（4-1）到式（4-10）看到。这里我们用模拟来验证每个状态是否在有界区域内^[9]。我们通过比较模拟结果和实验数据^[10]来验证控制律的性能。

图4-12 质子交换膜燃料电池的总体控制框图