模拟和实验测量结果对比分析

根据上述小信号线性状态空间模型，我们用MATLAB^®来模拟质子交换膜燃料电池的动态响应。这个燃料电池模型的主要参数值列于表3-4，对应着美国能源部国家能源技术实验室在西弗吉尼亚州摩根镇测试的一个燃料电池堆（包括四个电池）。根据辅助测量的估计，在式（3-40）中，电流密度单位小波动导致瞬态电压变化的Δi系数是30.762μΩm²。此外，在选定的负载电流40A工作点，根据输入和输出的稳态值可以计算状态变量的稳态值，然后再代入矩阵A，B，C和D。

表3-4　燃料电池模型的主要参数

下面的两个图比较了测试燃料电池堆能源部模型和Chiu等人模型的响应。在保持入口流率恒定的条件下，它们是输出电压对输入负载电流阶跃变化的响应。图3-11所示是第一个测试情况的结果，电池堆在稳态条件下运作，H_2in=3，664mL/min，N_2in+O_2in=11，548mL/min（假设均匀地分配给这四个电池），T=338.5K，负载电流是40A。在第五秒时，负载电流突然增加到50A，所测的电池堆输出电压（数据采集速率是每秒0.2个样品）快速降低，然后稳定在一个恒定值，这个过程伴随有一些“噪声”。我们使用能源部模型[式（3-41）]和Chiu等人的小信号模型[（式3-42）]来模拟这个40A工作电流的小波动。图3-11所示是测量的输出电压响应及能源部模型预测的输出电压响应和Chiu等人模型预测的输出电压响应（起始于工作点2.813V，在电流变化时，瞬态电压降是30.762Δi）。Chiu等人模型比能源部模型预测的值更好。

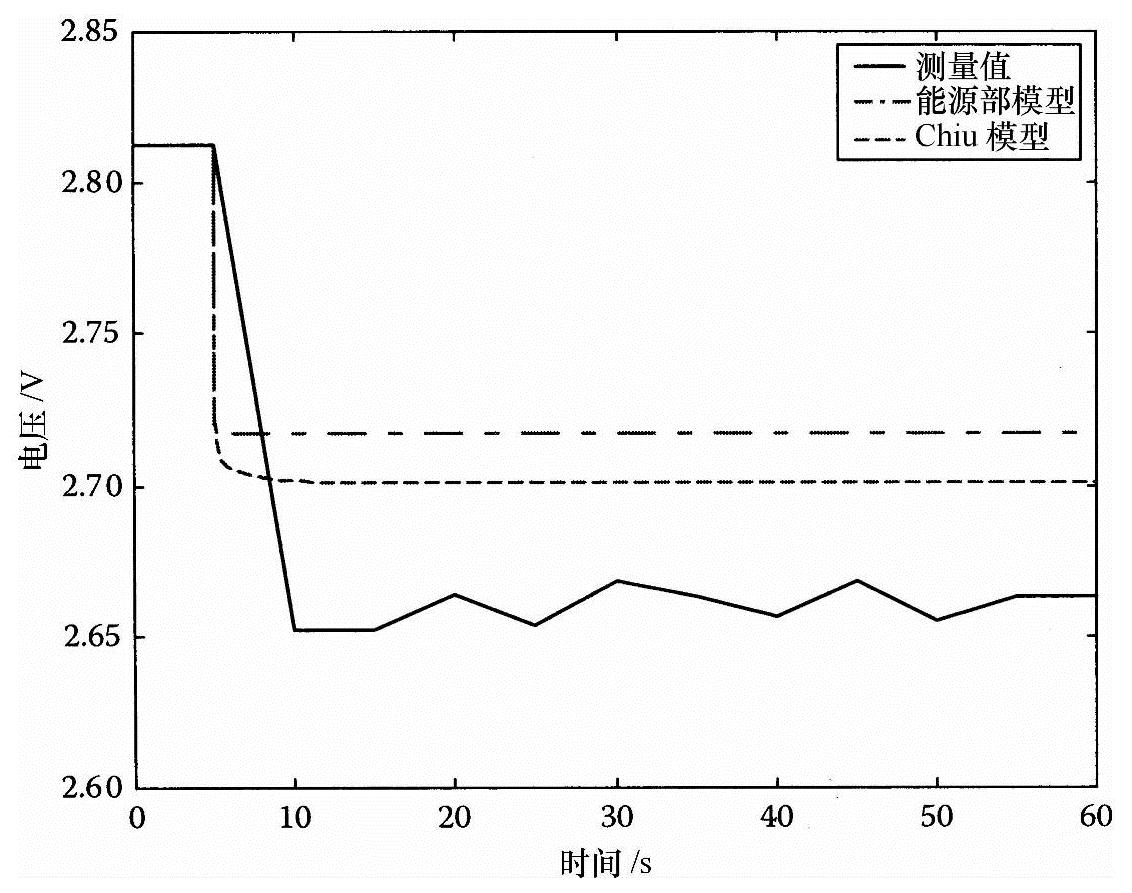
图3-11 模拟和测量结果比较 工作条件：H_2in=3664mL/min，N_in+O_2in=11，548mL/min，T（工作或电池温度）=338.5K；小波动：在第五秒，电流从40A突然增加到50A。(www.xing528.com)

请注意，测量与模拟稳态值的差异主要是由于精确输出电压表达式（3-19）的非线性。因为这个试验中的小波动相当大，所以我们可以预料电池堆的线性模型只是一个近似模型。

图3-12所示是第二个测试情况的结果，电池堆在稳态条件下工作，H_2in=3000mL/min，N_2in+O_2in=10，000mL/min（假设均匀地分配给这四个电池），T=338.5K，负载电流是40A。在0.1s，负载电流突然增加至42A，所测的电池堆输出电压（数据采集速率是每秒100个样品）快速降低，然后稳定在一个恒定值，这个过程伴随有一些“噪声”。我们使用能源部模型式（3-41）和Chiu等人的小信号模型式（3-42）来模拟这个40A工作电流的小波动。如图3-12所示，Chiu等人模型预测的瞬态响应和稳态输出电压比能源部模型更好。然而，两个模型之间响应的差异，及它们与实测响应的差异也减少了。这是我们所料到的，因为所选工作点的小波动（比上一个情况）小很多。

图3-12 又一个模拟和测量结果的比较 工作条件：H_2in=3000mL/min，N_2in+O_2in=10000mL/min，T（工作或电池温度）=338.5K；小波动：在0.1s时，电流从40A突然加到42A。

请注意，测量的输出电压响应在最初下跌后，随时间缓慢增加。在不同工作条件下，当负载增加后，都一致观察到这现象。而且小波动比大波动更容易观察到这现象（当使用更精细的电压刻度）。然而，这种现象似乎并不代表负脉冲和随后的恢复，因为它们属于线性动态系统。这可能是在负载变化后，膜含水量增加，电导率改变，导致电池电压逐渐增加。在今后的研究中需要解决这个问题。