燃料电池小信号模型优化

从式（3-19）和式（3-20）中，我们可以看到一些非线性项。为了使这些电池电压方程线性化，在燃料电池的一些特定工作点附近，用小波动法把动态模拟成线性系统，然后，对于输入值的小波动，可以很容易得到这些工作点的输出电压动态响应。

3.6.1.1.1 状态方程

首先，我们把氢气、氧气的和水（在阴极侧）的分压定义成系统状态变量。由于水管理是影响性能的因素，我们必须同时在阳极和阴极侧使用加湿器来控制电池内的湿度。阴极侧的水比阳极侧的水其影响更为复杂，因为它不仅包括从加湿器来的水，还包括反应副产品的水。图3-10表示流入流出电池的各种气体/水蒸气。

图3-10 质子交换膜燃料电池的气体/水蒸气流动示意图

根据理想气体定律PV=nPT，每个气体分压与电池内气体量成正比，而气体量等于入口气流率减去消耗气体量和出口气流率。因此，状态方程是

式中H_2in、O_2in和H₂O_Cin分别是氢气、氧气和阴极侧水的入口流率；H_2out、O_2out和H₂O_Cout分别是每种气体的出口流率。此外，H_2used、O_2used和H₂O_Cproduced代表气体使用率和产生率，它们与输出电流I的关系是

H_2used=2O_2used=H²O_Cproduced=2K_rI=2K_rA_ci （3-24）

式中 K_r=N/4F；

A_c——电池有效面积；

i——电池电流密度。

既然可以测量入口流率和输出电流，我们可以通过以下方程来确定出口流率

式中Anode_in是阳极入口流率和，Anode_in=H_2in+H₂O_Ain，Cath_in是阴极入口流率和Cath_in=N_2in+O_2in+H₂O_Cin。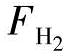、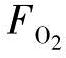和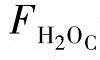分别是燃料电池内的每种气体的分压。在这里，我们要指出这个模型与原美国能源部（DOE）模型在定义压力分数上微妙却重要的差异^[31]。

在原美国能源部（DOE）模型中，

但在文献[32]提出的模型中，

在原美国能源部模型中，假设电池阳极和阴极的压力恒定在稳态的工作压力P_op。可是我们使用的模型是为了分析燃料电池的瞬态性能，必须考虑一旦改变了一些条件后，对每种气体气压的小波动。因此，我们在式（3-31）～（3-33）中使用气体分压的总和而不是假设工作压力恒定。

为了得到状态方程矩阵，我们把式（3-24）～（3-33）代入式（3-21）～（3-23），并在两侧求微分。(www.xing528.com)

举例说，我们将式（3-25）和式（3-28）代入式（3-21），就变成

接着，对给定的稳态工作点进行线性化（一阶近似）就会得到

式中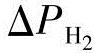、ΔH_2in和Δi是每个变量的小波动，而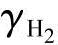是在阳极入口的氢气摩尔分数，定义为H_2in/Anode_in。此外，式中的状态变量和输入变量需要被选定工作点的稳态值取代。

根据这个例子，我们可以得到了能源部和Chiu等人模型的其他方程。

（i）原能源部模型

其中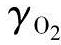是氧气在阴极入口的摩尔分数，定义为O_2in/Cath_in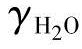，，是水在阴极入口的摩尔分数，定义为H₂O_Cin/Cath_in，因此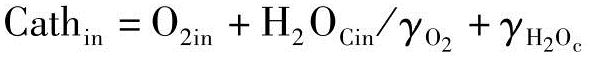（ii）Chiu等人的模型

式中 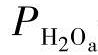——阳极的水蒸气分压；

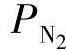——阴极的氮气分压；

对于燃料电池的输出，我们把式（3-20）代入式（3-19）并且在两侧求微分，就可以得到电池堆输出电压小波动ΔE的线性方程，

这是对特定工作点输入小波动的系统状态变化的响应。

3.6.1.1.2 线性状态空间模型使用式（3-34）～式（3-40），可以组成一个氢燃料电池线性小信号状态空间

模型：

式中，在Δx中的三个系统状态是电池内部氢气、氧气和水蒸气分压的小波动，在Δu中四个输入是氢气、氧气、水蒸气入口流率的小波动和输出电流密度；而系统的输出Δy是燃料电池堆电压的小波动。

对于能源部模型，矩阵A，B，C和D是

对于Chiu等人的模型，矩阵A，B，C和D是