质子交换膜燃料电池的状态空间动态模型优化方案

为了推导出一个简化的非线性动态燃料电池模型，我们做以下假设：

●由于电池堆温度的动态变化慢，假定平均电池堆温度是恒定的。

●可以很好地控制相对湿度略高于100%，因此液体水总能生成在电池堆。同时水箱和水分离器完美地控制这些液态水，可以避免水淹现象。

●反应物持续供给燃料电池，使它能在足够高的流率下工作。

●为了建立燃料电池的简化动态模型，假定入口反应物的摩尔分数是恒定的。换句话说，纯氢气（99.99%）被直接输入到阳极，氮气和氧气按21∶79的空气比例均匀混合输入到阴极。

●为了利用线性反馈，必须测量完全状态^[14]。

我们使用理想气体定律和摩尔守恒定律，定义氢气、阳极的水、阴极的氧气、氮气和水的分压为燃料电池的状态变量。图3-5表示入口气体和出口气体之间的关系^[15]。

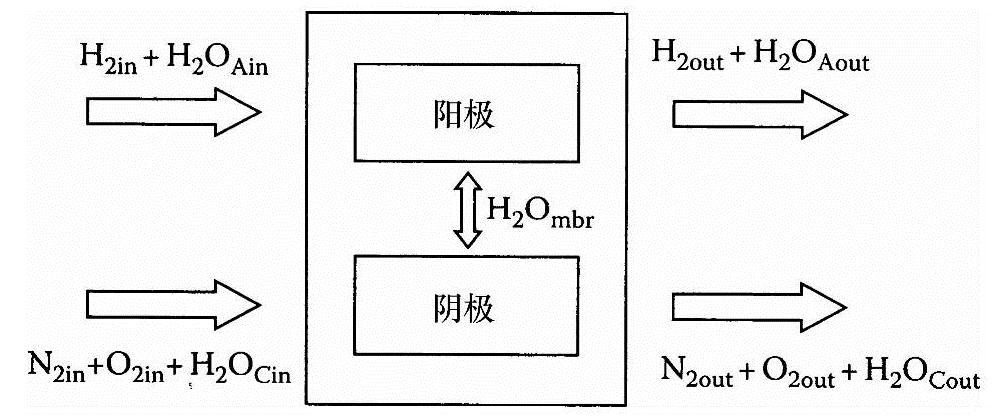
图3-5　质子交换膜燃料电池的气体流动示意图

下面的公式给出了分压的导数：

阳极摩尔守恒

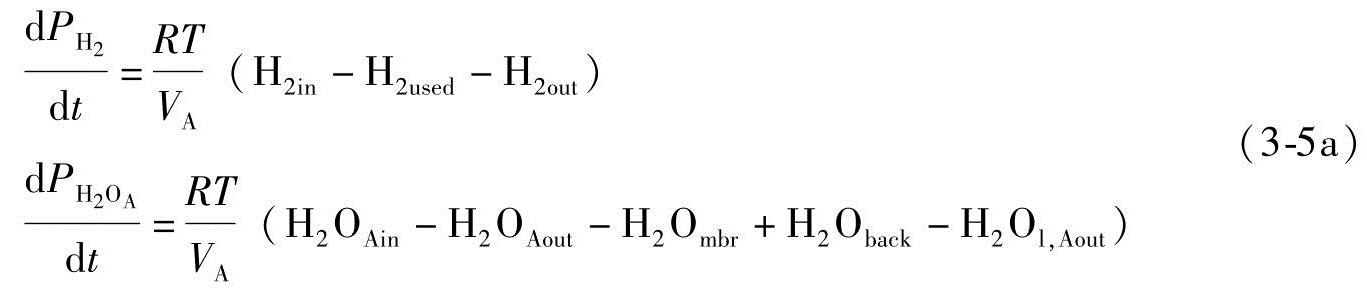
阴极摩尔守恒

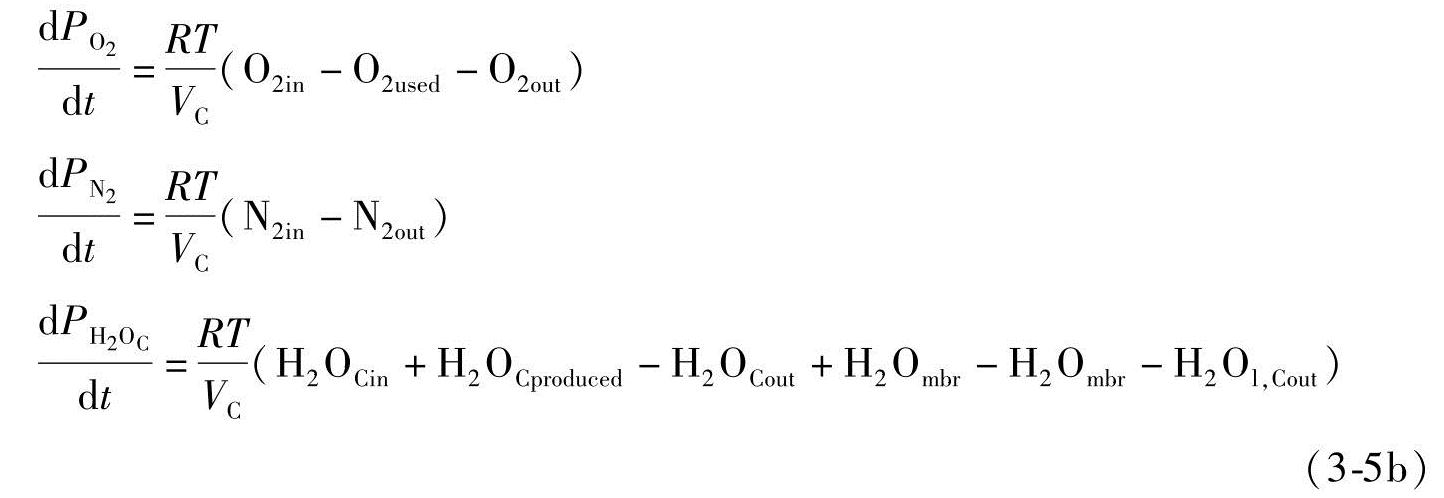
式中H_2in、O_2in、N_2in、H₂O_Ain和H₂O_Cin分别是氢气、氧气、氮气、阳极侧、阴极侧水的入口流率。此外，H_2out、O_2out、N_2out、H₂O_Aout和H₂O_Cout是每种气体的出口流率。H_2used、O2used和H₂O_Cproduced分别是气体的使用率和产生率。一般来说，入口水流过膜的流率H₂O_mbr是电池堆电流和膜含水量λ_m的函数。假定λ_m=14^[7，16]，H₂O_mbr只是电流密度的函数^[7，16]，并且H₂O_mbr=1.2684（N·A_fc·I_fc）/F，其中A_fc（cm²）是燃料电池的有效面积，N是燃料电池的数量，I_fc是燃料电池的电流密度。此外，为了更准确地描述一个动态模型，可以定义水从阴极向阳极的回流为H₂O_v，back=γ·H₂O_v，mbr^[2]。当含水量λ_m=14时，回流系数β的测量值是6×10^-6（cm²/s）^[2]。液体水离开阳极和阴极的流率是H₂O_l，Aout和H₂O_l，Cout。它们取决于每种气体的饱和程度^[7]。为了估计液体水，必须用水蒸气饱和压力来计算水蒸气最大质量，公式如下：

饱和压力p_vs可以根据文献[17]中的一个公式计算：

log₁₀（p_vs）=-1.69×10^-10T⁴+3.85×10^-7T³-3.39×10^-4T²+0.143T-20.92 （3-7）

式中饱和压力p_vs的单位是kPa，温度T的单位是K。如果式（3-5a）和式（3-5b）中水的质量比式（3-6）中最大水蒸气质量大，可以同时形成液体水。液体水和水蒸气质量的计算方法如下^[7]：

逻辑1

如果m_{w，A or C}≤m_{v，max A or C}→m_{v，A or C}=m_{w，A or C}，m_{l，A or C}=0；

如果m_{w，A or C}＞m_{v，max A or C}→m_{v，A or C}=m_{v，max A or C}；

m_{l，A or C}=m_{w，A or C}-m_{v，max A or C}

因此，β_{A or C}可以用来估计在方程（3-8）中液态水的形成。根据逻辑1，如果m_{w，A or C}≤m_{v，max A or C}，那么β_{A or C}=0；否则β_{A or C}=1，因此，H₂O_l，Aout和H₂O_l，Cout定义如下

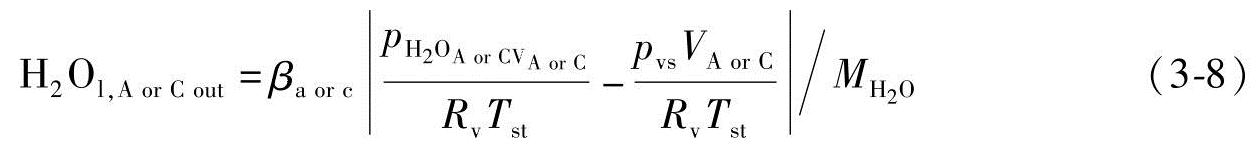
式中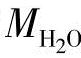是水的摩尔质量，为18.02g/mol。我们定义所有的流率、气体使用率和产生率的单位是mol/s。然而，由于我们假设相对湿度都超过100%，水是液态的，β_{A or C}是1，这意味着在模拟中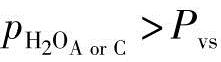。V_A和V_C分别是阳极和阴极的体积，它们的单位是m³。根据电化学的基本关系，使用和产生的气体是电池电流密度的函数^[4]：

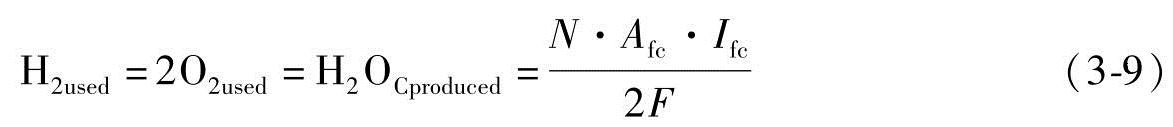(www.xing528.com)

为了简化起见，我们定义

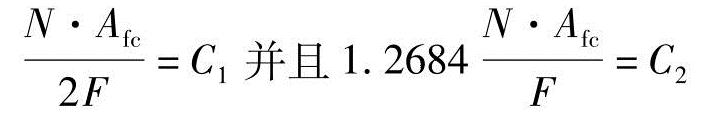
因此，在式（3-5a）和式（3-5b）中，H₂O_mbr和H₂O_v，back可以用C₁和C₂简化。有了实测的入口流率和电池堆电流，出口流率就是阳极和阴极入口流率Anode_in和Cath_in，减去气体使用率和产生率以及文献[13]中提出的压力分数。Anode_in的定义是H_2in+H₂O_Ain，Cath_in的定义是O_2in+N_2in+H₂O_Cin。

阳极侧出口流率是

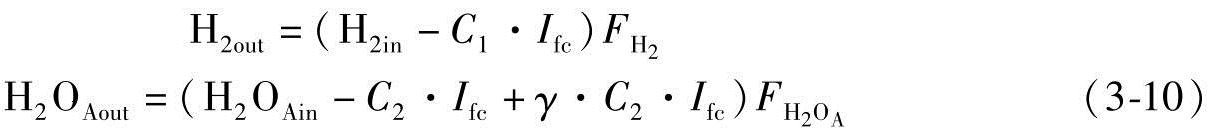
阴极侧出口流率是

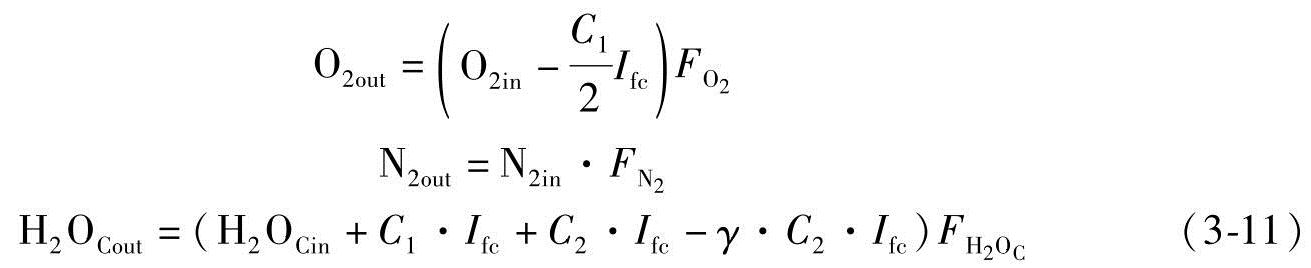
式中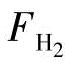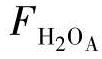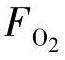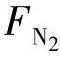，，，和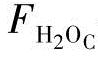分别是燃料电池内各种气体的压力分数，给出如下^[18]：

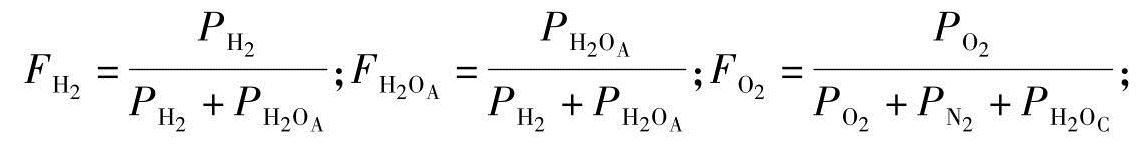
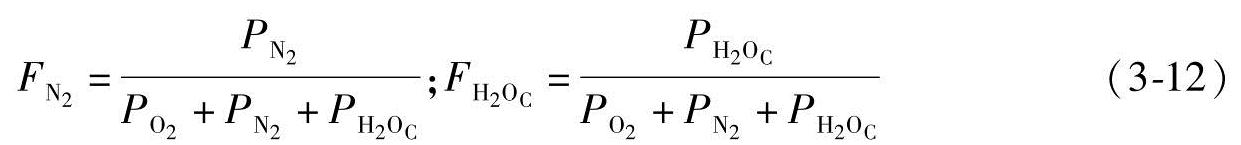
为了分析燃料电池的瞬态性能，我们要考虑到Chiu等人提出的每种气体的压力分数^[18]。在文献[18]中，只考虑到3种压力分数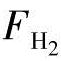、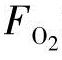和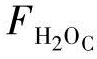。但在我们的研究中，考虑到了所有气体的压力分数，因此得到更精确的燃料电池动态模型和比以往研究^{[3，7，18，19]}更好的燃料电池瞬态特性分析。把式（3-10）和式（3-12）代入式（3-5a）和式（3-5b），可以得到状态方程[式（3-13）和式（3-14）]。

阳极侧新的状态方程是

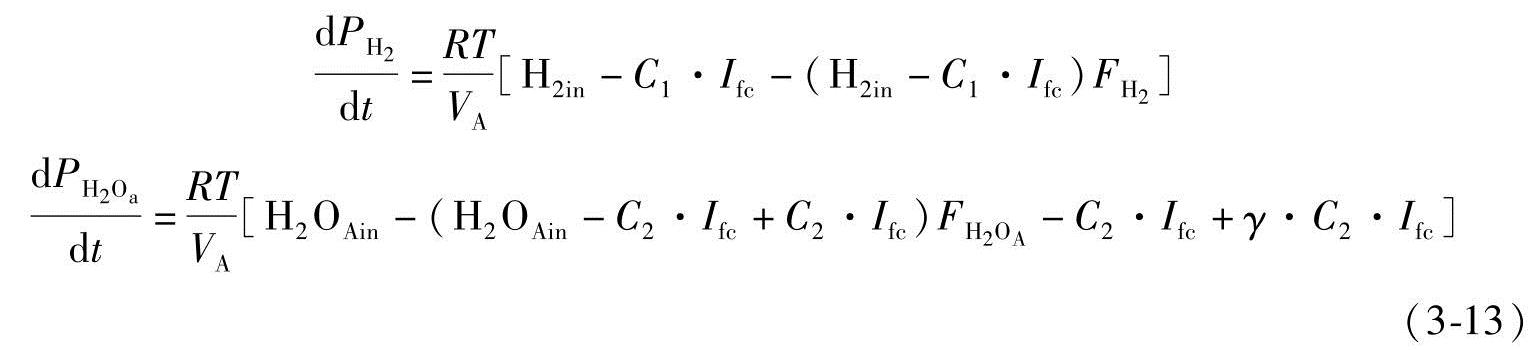
阴极侧新的状态方程是

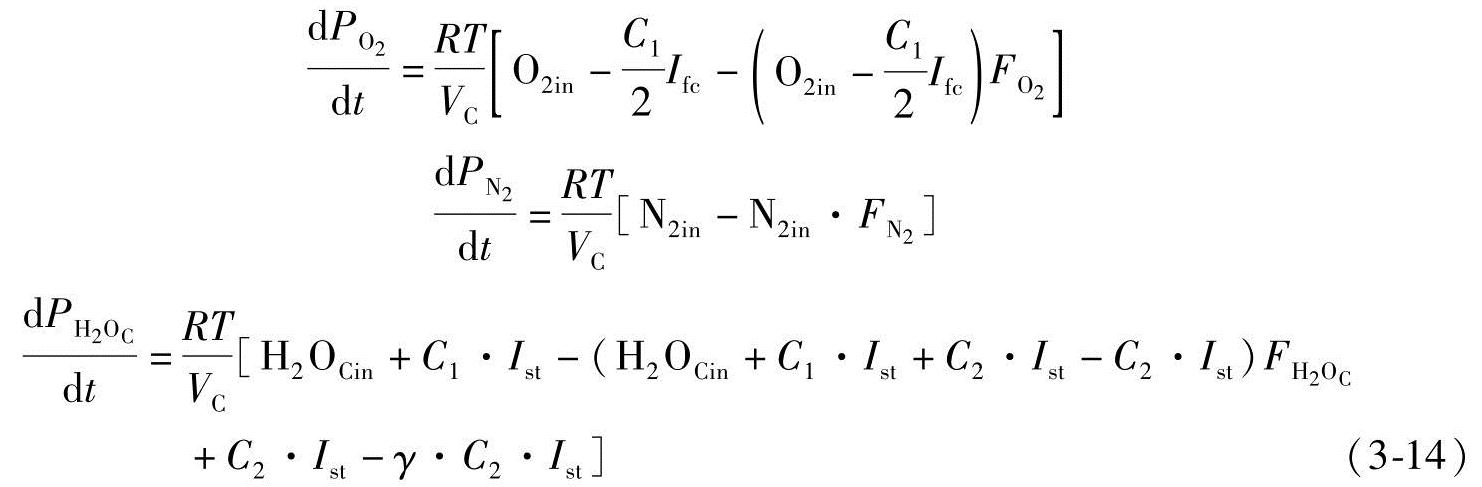
因为初始摩尔分数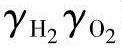和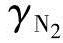分别被设为0.99，0.21和0.79^[3，7，19]，所以输入值H_2in，O_2in和N2_in由摩尔分数定义如下：

在阳极和阴极入口，水流率可以用相对湿度、饱和压力和每侧的总压力来表达如下^[2]：

式中，φ_a和φ_c分别是在阳极和阴极侧的相对湿度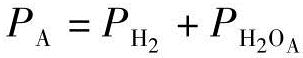，是阳极分压的总和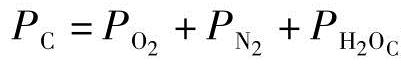，是阴极分压的总和。P_vs是饱和压力，可以在热力学表中找到^[20]。相对湿度φ_a和φ_c，可以由阳极注入水u_{a_ h}和阴极注入水u_{c_ h}来定义。此外，Anode_in和Cath_in分别定义为输入控制变量u_a和u_c与每侧转换因子k_a和k_c的乘积^[11，18]，单位也由标准升/秒（L/s，Standard Liters Per Minute，SLPM）变为摩尔/秒（mol/s）。换句话说，

Anode_in=u_a·k_a

Cath_in=u_c·k_c （3-17）

式中的转换因子k_a和k_c分别是0.065mol/s。假定氢气和空气化学计量比是恒定的，这样可以保证这两种反应物被持续送入并流过电池堆^[20]。因此，燃料电池控制主要依靠输入控制变量u_a和u_c。首先，阳极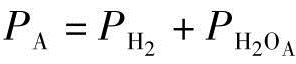气压和阴极气压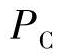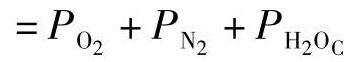将分别由u_a和u_c控制，以避免不必要的压力波动，防止膜电极组件的损坏，帮助延长燃料电池堆的寿命^[15]。因为注水系统有一个非常缓慢的时间常数τ_d约70s^[21]，我们可以用一阶时间延迟注入水u_a__h和u_c__h来控制两侧的相对湿度。因此，在燃料电池动态模型中，我们为水注入使用一阶时间延迟模型，水注入输入和相对湿度关系的状态方程可以推导如下：

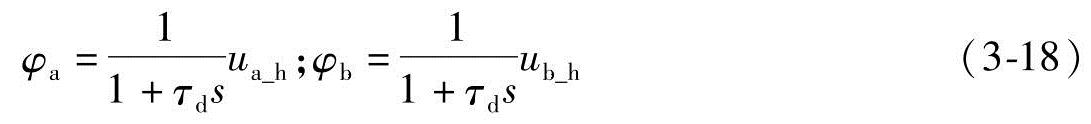
式中φ是相对湿度。从式（3-16）可以看到，每个水注入输入是湿度的函数，水注入输入也影响压力的控制。因此，可以建立一个质子交换膜燃料电池的动态模型。我们将在第四章详细描述控制设计。