载波相位测量技术

（1）原理

利用GPS卫星发射的载波为测距信号。由于载波的波长（λ_L1=19.03cm，λ_L2=24.42cm）比测距码波长要短得多，因此对载波进行相位测量，就可能得到较高的测量定位精度。

假设卫星S在t₀时刻发出一载波信号，其相位为φ（S）；此时若接收机产生一个频率和初相位与卫星载波信号完全一致的基准信号，在t₀瞬间的相位为φ（R）。假设这两个相位之间相差N个整周信号和不足一周的相位Fr（ψ），则相位差为

φ（R）-φ（S）=Fr（ψ）+N

载波信号是一个单纯的余弦波。在载波相位测量中，接收机无法判定所量测信号的整周数，但可精确测定其零数Fr（ψ），并且当接收机对空中飞行的卫星作连续观测时，接收机借助于内含的多普勒频移计数器，可累计得到载波信号的整周变化数Int（ψ）。因此，ψ=Int（ψ）+Fr（ψ）才是载波相位测量的真正观测值。而N₀称为整周模糊度，它是一个未知数，但只要观测是连续的，则各次观测的完整测量值中应含有相同的，也就是说，完整的载波相位观测值应为

ψ～=ψ+N₀=Int（ψ）+Fr（ψ）+N₀

在t₀时刻首次观测值中Int（ψ）=0，不足整周的零数为Fr（ψ），N₀是未知数；在t₁时刻N₀值不变，接收机实际观测值ψ由信号整周变化数Int（ψ）和其零数Fr（ψ）组成。

与伪距测量一样，考虑到卫星和接收机的钟差改正数V_a、V_b以及电离层折射改正和对流层折射改正δρI，δρT的影响，可得到载波相位测量的基本观测方程为：ρ=ψ～·λ，λ为载波波长。代入伪距方程中，得

两式比较可看出，载波相位测量观测方程中，除增加了整周末知数N₀外，与伪距测量的观测方程在形式上完全相同。

（2）周跳与整周未知数

1）周跳(www.xing528.com)

如果由于某种原因在两个观测历元之间的某一段时间工作计数器中止了正常的累积工作，从而使整周计数较应有值少了n周，那么当计数器恢复正常工作后，所有的载波相位观测值中的整周计数Int（ψ）便都会含有同一偏差值——较正常值少n周。这种整周计数Int（ψ）出现系统偏差而不足一周的部分Fr（ψ）仍然保持正确的现象称为整周跳变，简称周跳。

2）周跳的探测与修复

卫星在空间的运行轨迹是一条平滑的曲线，因而卫星至接收机的载波相位观测值的变化也应是平缓而有规律的。周跳破坏这种规律性，使观测值产生一种系统性的误差。周跳的探测及修复从本质上讲就是如何从载波相位观测值的时间序列中寻找可能存在的这种系统性的粗差并加以改正。探测、修复周跳的方法很多，较为常用的有高次差法、多项式拟合法、利用双频P码伪距观测值等方法。

高次差法：在相邻观测值之间依次求差，一般取三次差，若无周跳，所得结果应在同一量级，否则，会有较大差异。该法虽较为直观，易于理解但不太适合在计算机上运算。

多项式拟合法：从本质上讲与高次差是一致的，其算法适合于计算机运算，被广泛采用。其作法是将n个无周跳的载波相位观测值代入下式，进行拟合：

用最小二乘法求得式中的系数a₀，a₁，a₂，…a_n，并根据拟合后的残差V_i计算出中误差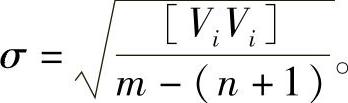用求得的多项式系数外推下一历元的载波相位观测值并与实际观测值进行比较，当两者之差小于3σ时，认为无周跳。但不足整周部分要保持不变。

用双频P码伪距观测值来探测、修复周跳：根据任一历元的双频P码伪距观测值P₁、P₂及载波相位观测值ψ₁、ψ₂，即可求得宽巷观测值的整周未知数N，若相邻两历元所得整周未知数之差小于4σ，则认为不存在周跳。

采用该方法时无需提供卫星轨道、测站坐标等信息，也不需要在测站和卫星间求差，适用于任意长度的基线。与此同时，还可完成粗差的探测和剔除工作，是一种较为理想的方法。该方法在自动化数据编辑中得到了广泛应用。

3）整周未知数

整周未知数的确定是载波相位测量中特有的问题，也是进一步提高GPS定位精度、提高作业速度的关键所在。目前，确定整周未知数的方法主要有三种：伪距法、N₀作为未知数参与平差法和三差法。伪距法就是在进行载波相位测量的同时，再进行伪距测量；由两种方法的观测方程可知，将未经过大气改正和钟差改正的伪距观测值减去载波相位实际观测值与波长的乘积，便可求出整周未知数N₀，N₀作为未知数参与平差，就是将N₀作为未知参数，在测后数据处理和平差时与测站坐标一并求解；根据对N₀的处理方式不同，可分为“整数解”和“实数解”。三差法就是从观测方程中消去N₀的方法，又称多普勒法，因为对于同一颗卫星来说，每个连续跟踪的观测中，均含有相同的整周未知数，因而将不同观测历元的观测方程相减，即可消去整周未知数N₀，从而直接解算出坐标参数。