高精度面积量算方法：三角形、梯形、长方形与坐标解析法

在各种工程规划设计中，时常遇到测算面积的工作，如求流域面积、汇水面积、断面面积等。面积量算的方法很多，下面介绍几种常用方法。

8.5.4.1 几何图形法

适用于图上外形规整的多边形的面积量算。

将多边形划分为若干个简单的几何图形，如三角形、梯形、长方形等。从图上解出图形各要素（长、宽、高等），根据地形图比例尺换算成实地长度，然后按相应几何图形的公式计算面积，最后将所有图形的面积相加得到整个多边形的面积。如图8-28所示，将多边形划分为若干个三角形和梯形。划分为三角形时，面积量算的精度较高，其次为梯形、长方形。

8.5.4.2 方格法

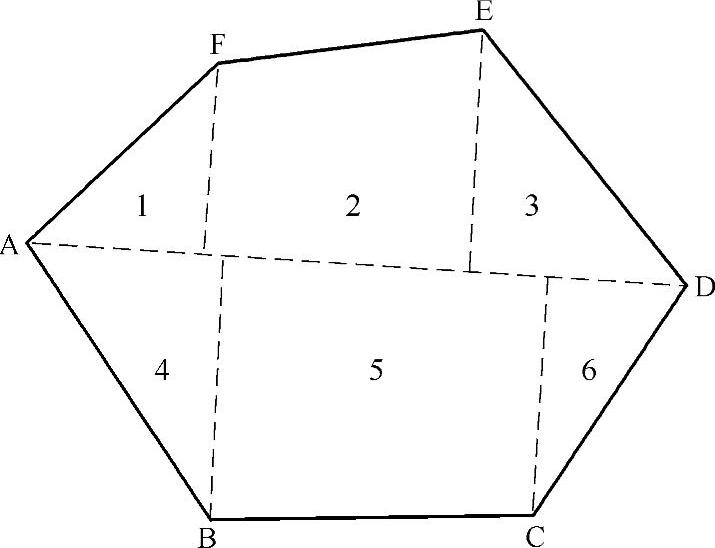
图8-28 几何图形法求面积

对于不规则曲线所围成的图形，可采用方格法进行面积量算。如图8-29所示，用透明方格网纸（方格边长为1mm、2mm、5mm或1cm）蒙在要量测的图纸上，先数出图形内的完整方格数，然后将不完整的方格用目估法折合成整方格数，两者相加乘以每格所代表的面积值，即为所量图形的面积。计算公式为

S=n·A （8-14）

式中 n——方格总数；

A——1个方格的实地面积。

图8-29中，方格边长为1cm，图的比例尺为1∶1000，则A=（1cm）2×1000²=100m²。完整的方格数为36个，不完整的方格凑整为8个，方格总数为44个，则所求图形的实地面积为

S=44×100m²=4400m²

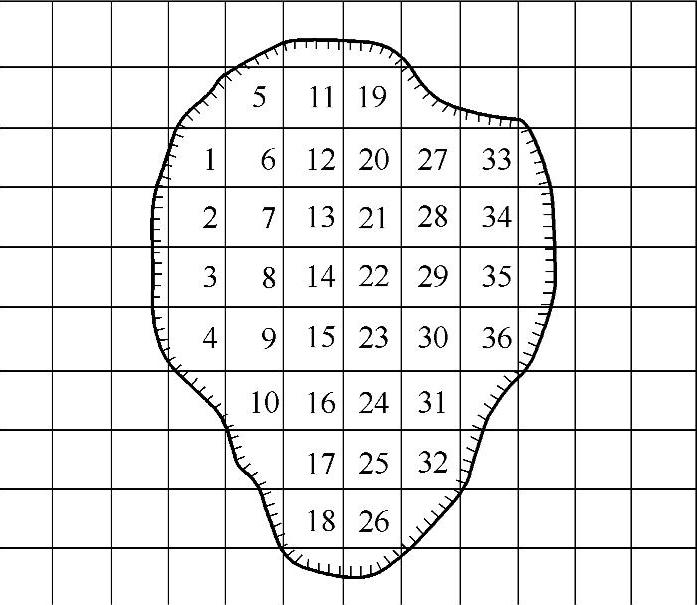
图8-29 方格法求面积

8.5.4.3 平行线法

(www.xing528.com)

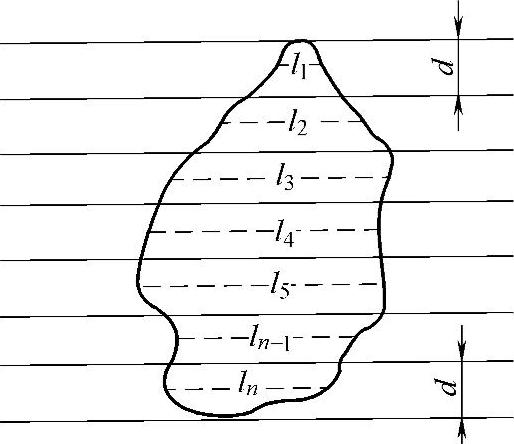
图8-30 平行线法求积

方格网的量算受到方格凑整误差的影响，精度较低，为提高量算精度，可采用平行线法。如图8-30所示，将绘有等间距（1mm或2mm）平行线的透明膜片（或透明纸）覆盖在待测图形上，则图形被分割成若干个近似梯形，梯形的高就是平行线的间距d，图内平行虚线是梯形的中线。量出各中线的长度，就可以按下式求出图上面积。

A=l₁×d+l₂×d+…+l_n×d=d×Σl（8-15）

将图上面积化为实地面积时，如果是地形图，应乘上比例尺分母的平方；如果是纵横比例尺不同的断面图，则应乘上纵横两个比例尺分母之积。

例如在1∶2000的地形图上，量得某图形的全部中线长Σl=57.8cm，d=1mm，则此图形的实地面积为A=d×Σl×M²=1.0×10^-3×57.8×10^-2×2000²=578m²

8.5.4.4 解析法

当要求量算精度较高时，可应用坐标解析法。如图8-31所示。

对于n点多边形，其面积公式的一般形式为

S=1/2∑x_i（y_i-1-y_i+1） （8-16）

或者 S=1/2∑y_i（x_i+1-x_i-1） （8-17）

可同时用两式计算，以便检核。注意应用该公式时，多边形点号为顺时针编号。

8.5.4.5 求积仪法

求积仪是一种专供量算图形面积的仪器。其特点是：操作简便，量算速度快，能保证一定的精度，并适用于各种不同图形的面积量算。

求积仪分两大类：机械求积仪和电子求积仪。

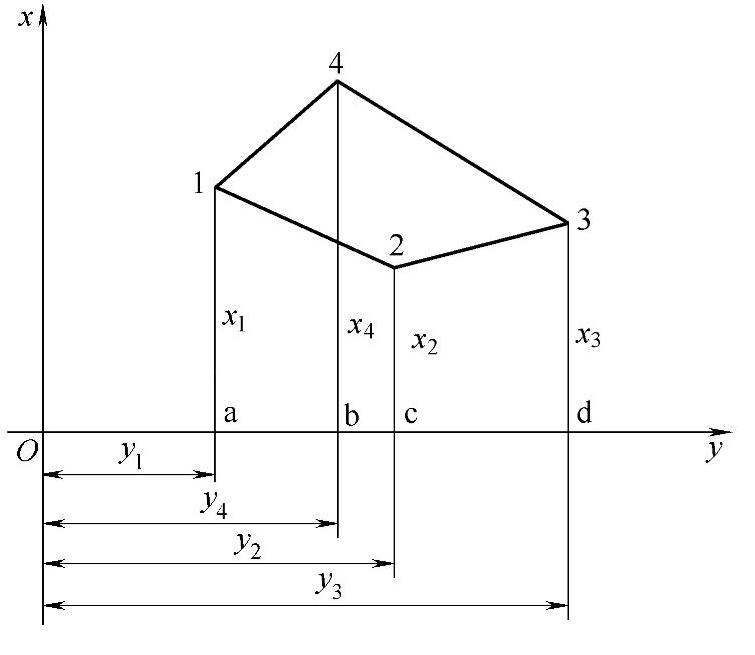
图8-31 坐标解析法计算面积原理