导线测量内业计算方法总结

导线测量外业结束后，就要进行导线内业计算。在内业计算之前，要全面检查外业观测数据有无遗漏，记录计算是否正确，成果是否符合限差要求，要保证原始数据的正确性，以免造成不必要的计算返工。还要根据外业成果绘制导线计算示意图（如图7-7所示），示意图上应注明导线点点号和相应的角度和边长，起始方位角及起算点的坐标。计算时要在相应的导线计算表中进行，先按顺序填好点号，再将有关数据写在相应的栏目中。

7.2.3.1 闭合导线计算

闭合导线是由折线组成的多边形。因而，闭合导线必须满足两个几何条件：一个是多边形内角和条件；另一个是坐标条件，即从起算点开始，逐点推算导线点的坐标，最后推回到起算点，由于是同一个点，因而推算出的坐标应该等于已知坐标。闭合导线计算的方法步骤如下，根据计算方法与步骤填写表7-2：

1.角度闭合差的计算与调整

由平面几何知识可知，n条边的多边形，内角和的理论值应为

∑β_理=（n-2）×180° （7-1）

设闭合导线实测内角的总和为∑β_测。由于在角度观测过程中，不可避免地会产生误差，测得的内角总和不可能刚好等于内角和的理论值，两者的差值称为角度闭合差。设角度闭合差用f_β表示，则

f_β=∑β_测-∑β_理 （7-2）

例如图7-7的闭合导线，其角度闭合差为f_β=360°00′38″-360°=+38″。角度闭合差f_β的大小一定程度上标志着测角的精度。

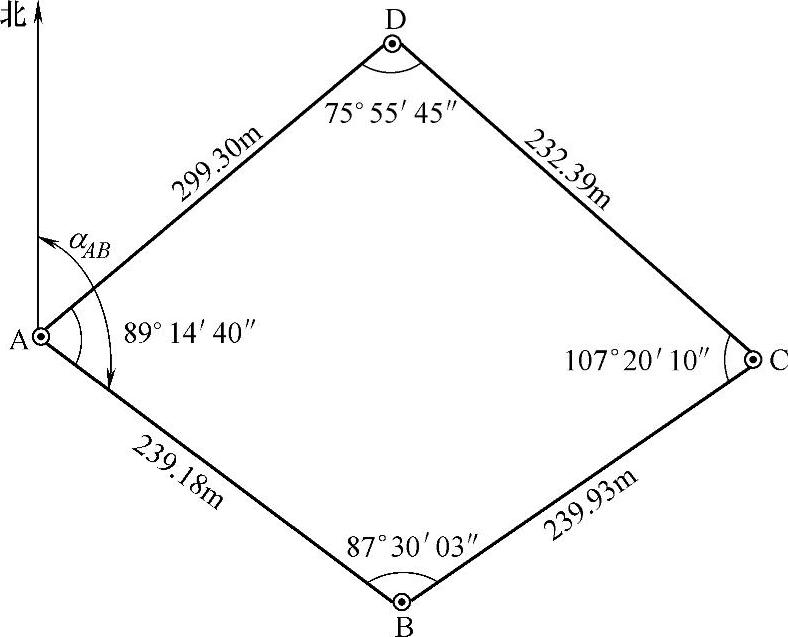
图7-7 闭合导线计算示意图

当角度闭合差不大于容许值时，可将闭合差按相反符号平均分配到观测角中。每个角度的改正数用V_β。即

V_β=-f_β/n （7-3）

式中f_β——为角度闭合差，（″）；

n——为闭合导线内角个数。

如果f_β的数值不能被导线内角数整除而有余数时，可将余数调整分配在短边的邻角上，使调整后的内角和等于∑β_理。

如果角度闭合差超过容许值，应分析原因，进行外业局部或全部返工。

本例的角度闭合差容许值为f_β容=±60 n=±604=±120″，显然f_β<f_β容，可以进行角度闭合差调整分配。

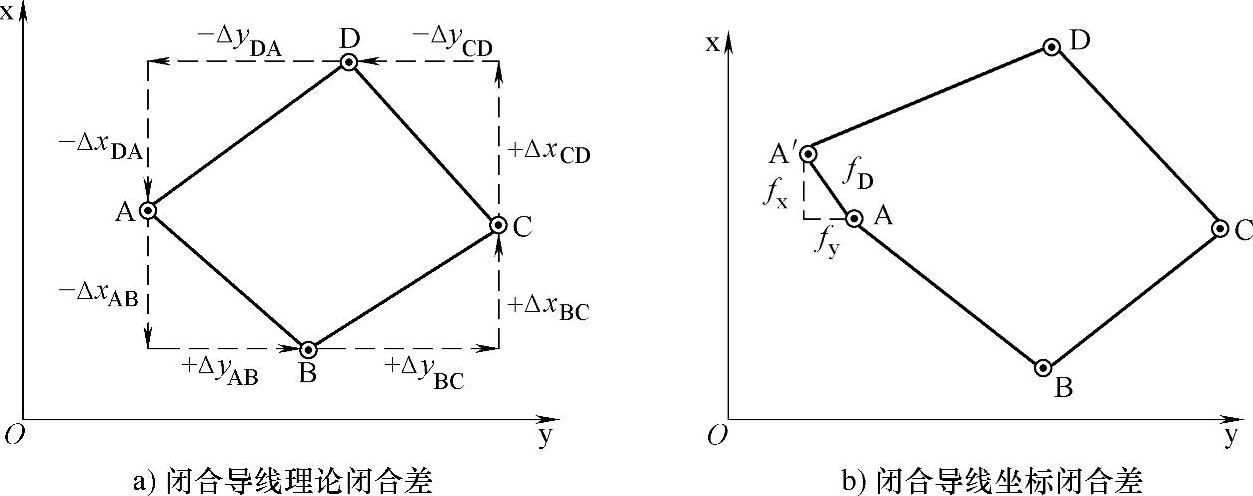
图7-8 闭合导线坐标闭合差

2.导线边方位角的推算

由起算边方位角，再结合改正后的角度值，可用方位角计算公式推算各边的方位角，即

α_前=α_后+β_左±180°

α_前=α_后-β右±180° （7-4）

式中，若α_后+β_左算得的角度值大于180°，则减去180°（在减去180°之后，若还大于360°，再减去360°）；若算得的角值小于180°，则加180°。

如图7-9算例中的BC边的方位角为

α_BC=α_AB+β_B-180°=133°46′40″+87°29′54″-180°=41°16′34″

为了检核方位角计算有无错误，方位角应推回到起算边，因多边形已调整角度闭合差，故应等于起算边的方位角，否则，应查明原因，加以纠正。

3.坐标增量计算

坐标增量的计算按下述计算公式计算，即

Δx_i=D_i·cosα_i

Δy_i=D_i·sinα_i

例如算例中BC边的坐标增量为

Δx_BC=D_BC×cosα_BC=239.93×cos（41°16′34″）=180.32m

Δy_BC=D_BC×sinα_BC=239.93×sin（41°16′34″）=158.28m

计算位数取至厘米。

4.坐标增量闭合差的计算与调整

闭合导线每一条边的坐标增量计算出后，由图7-8a可以看出，闭合导线各边纵、横坐标增量的代数和在理论上应等于零，即

∑Δx_i=0 ∑Δy_i=0 （7-5）

由于测量角度和边长均存在误差，尽管角度进行了闭合差的调整，但调整后的角度值也不一定是该角的真值。所以，由边长和方位角计算出的纵、横坐标增量，其代数和∑Δx_测和∑Δx_测一般都不等于零，而等于某个数值，这两个数值分别称为闭合导线纵坐标增量闭合差和横坐标增量闭合差，用f_x和f_y分别表示，则

f_x=∑Δx_测f_y=∑Δy_测 （7-6）

由于存在f_x和f_y，使闭会导线由A点出发最后不是闭会到A点，而是落在A′点，产生了一段差距AA′，这段差距称为导线全长闭合差，用f_D表示，如图7-8b。从图中可知

导线全长闭合差f_D主要由量边误差引起，一般来说，导线越长，全长闭合差也越大，因而单纯用导线全长闭合差f_D还不能正确反映导线测量的精度，通常采用f_D与导线总长∑D的比值并化成分子为1的分式来表示，称为导线全长相对闭合差，来衡量导线测量的精度好坏，用K表示为

K=f_D/∑D=1/∑D/f_D （7-8）

图根导线测量中，一般情况下，K值不应超过1/2000；困难地区也不应超过1/1000。若K值不满足限差要求，首先检查内业计算有无错误，其次检查外业成果，若均不能发现错误，则应到实地现场重测可疑成果或全部重测；若K值满足限差要求，可进行坐标增量闭合差的调整。

由于坐标增量闭合差主要由边长误差影响而产生的，而边长误差大小与边长的长短有关，因此，坐标增量闭合差的调整方法是将增量闭合差f_x、f_y反号，按与边长成正比分配于各个坐标增量中，使改正后的∑Δx、∑Δy均等于零。设第i边边长为D_i，其纵、横坐标增量改正数分别用V_Δxi、V_Δyi表示

V_Δxi=-f_x/∑D·D_i

V_Δyi=-f_y/∑D·D_i （7-9）

式中 V_Δxi——第i边的纵坐标增量，单位为m；

V_Δyi——第i边的横坐标增量，单位为m；

∑D——导线边长总和，单位为m。(www.xing528.com)

改正数一般取至厘米，坐标增量改正数总和应等于坐标增量闭合差的相反数，用此进行检核。

5.导线点坐标计算

坐标增量调整后，可根据起算点的坐标（独立地区是假定坐标）和调整后的坐标增量，逐点计算导线点的坐标，计算公式为

x_前=x_后+Δx_i

y_前=y_后+Δy_i （7-10）

式中 x_前、y_前——第i边前一点的纵、横坐标，单位为m；

x_后、y_后——第i边后一点的纵、横坐标，单位为m；

Δx_i、Δy_i——第i边的纵、横坐标增量，单位为m。

按上式计算完闭合导线最后一个点的坐标后，还要再推算出起算点的坐标，看是否与已知坐标相等，以检查计算是否正确。

7.2.3.2 附合导线的计算

附合导线的计算与闭合导线的计算基本上相同，现仅将其不同的两点说明如下：

（1）附合导线不是闭合多边形（如图7-9所示），角度闭合差用推算坐标方位角的方法来计算方位角闭合差。

如图7-9所示，设A、B、C、D为已知点，α_AB为起算边的已知方位角，α_CD为终边的已知坐标方位角。根据方位角的推算公式如下。

α₁₂=α_AB+β₁-180°

α₂₃=α₁₂+β₂-180°=α_AB+（β₁+β₂）-2×180°

︙

α_CD′=α_（n-1）n+β_n-180°=α_AB+（β₁+β₂+…+β_n）-n×180°

即 α_CD′=α_AB+∑β_i-n×180° （7-11）

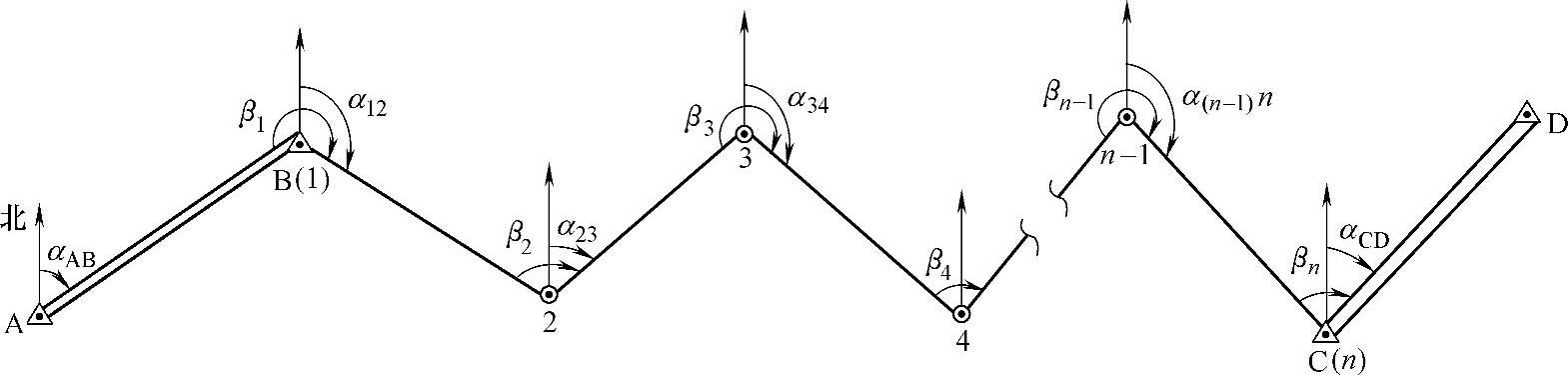
图7-9 附合导线计算图

式中 n——观测角个数。

由于观测角度误差的影响，推算出的方位角α_CD′与已知方位角α_CD一般不相等，产生了方位角闭合差f_β，即

f_β=α_CD′-α_CD

故附合导线方位角闭合差的计算公式为

f_β=α_AB+∑β_i-n×180°-α_CD

写成一般形式为

f_β=∑β_i-n×180°+α_起-α_终 （7-12）

式中 α_起——附合导线的起算边方位角，（°）；

α_终——附合导线的终边方位角，（°）；

f_β——方位角闭合差，（″）；

n——附合导线转折角个数。

例如，图7-10为一条附合导线，已知BA边的方位角α_BA=149°40′00″，CD边的方位角α_CD=8°52′55″，四个观测角总和∑β=579°13′36″，则

f_β=579°13′36″-4×180°+149°40′00″-8°52′55″=+41″

附合导线方位角闭合差的容许值和调整方法与闭合导线相同，根据以下计算步骤与方法填写表7-3。

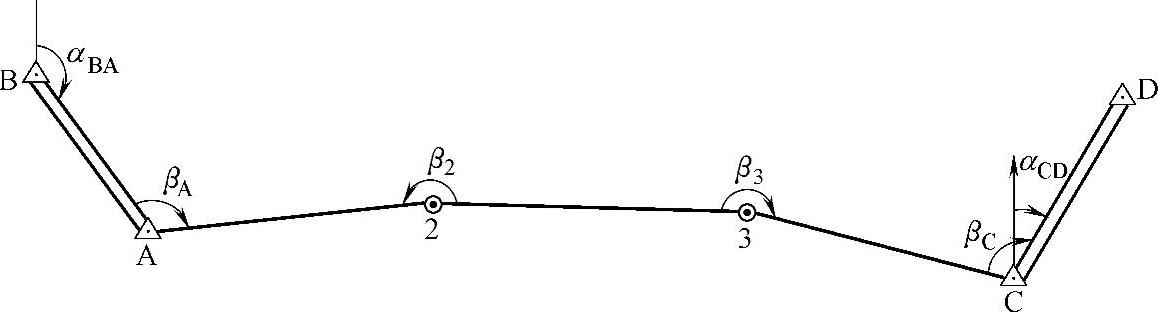
图7-10 附合导线算例图

（2）附合导线是从一已知点出发，附合到另一个已知点，因此，纵、横坐标增量的代数和理论上不是零，而应等于起、终两已知点间的坐标增量（即两点坐标之差）。如不相等，其差值即为附合导线的坐标增量闭合差，计算公式为

f_x=∑Δx_测-（x_终-x_起）

f_y=∑Δy_测-（y_终-y_起） （7-13）

式中 x_起、y_起——分别为附合导线起始点的纵、横坐标，单位为m；

x_终、y终——分别为附合导线终点的纵、横坐标，单位为m。

在图7-10算例中，纵、横坐标增量闭合差为

f_x=-330.19-（475.60-806.00）=+0.21m

f_y=438-（1223.10-758.00）=+0.11m

算出了f_x和f_y以后，其余的计算与闭合导线完全相同。

（3）支导线的坐标计算

由于支导线只是一端与已知点相连，而另一端不附合到任何已知点，因而它就没有几何条件的约束，其坐标计算不必进行角度闭合差和坐标增量闭合差的调整，直接由各边的边长和方位角求坐标增量，最后依次求各点的坐标。

表7-2 闭合导线坐标计算表

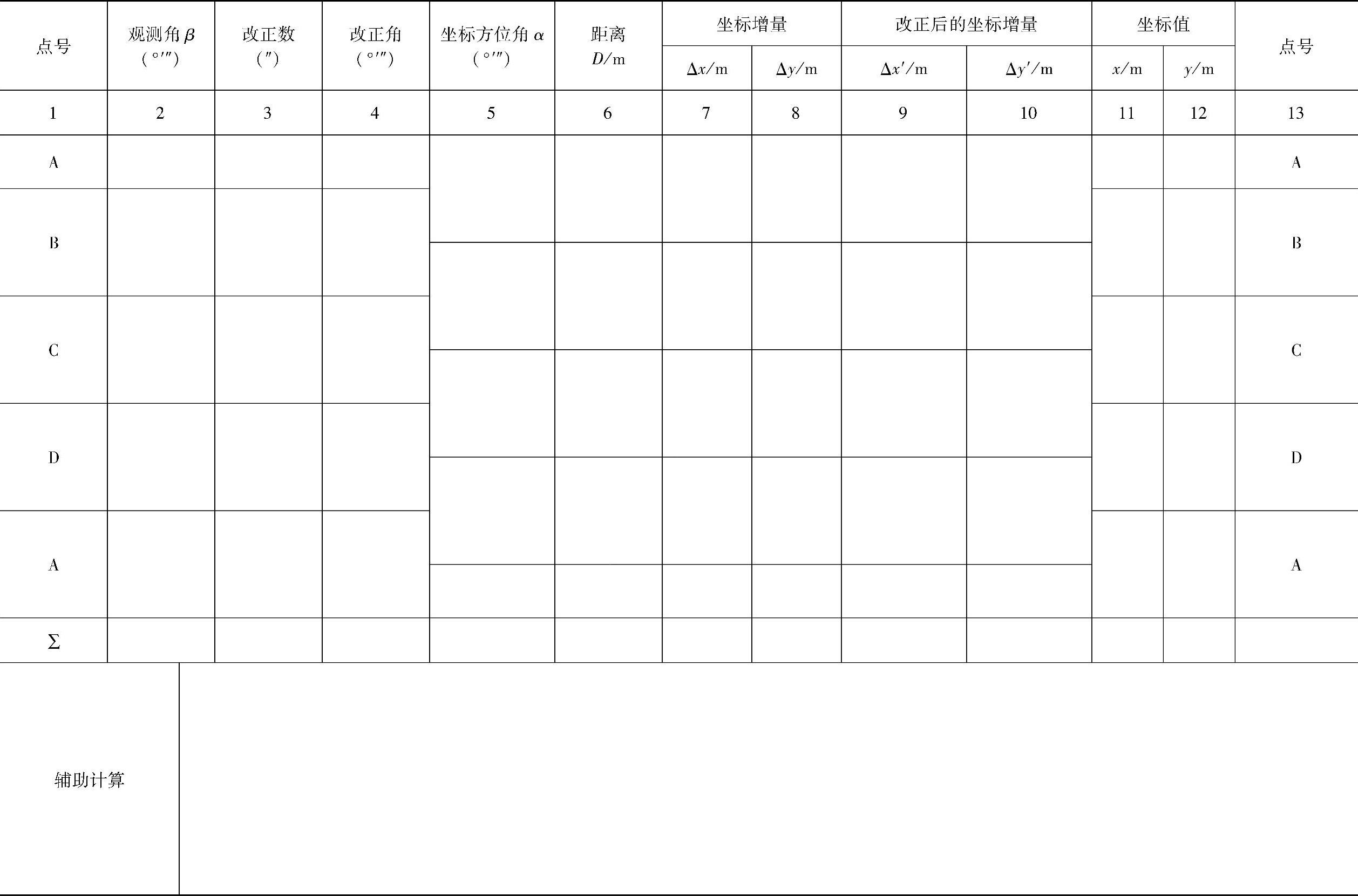
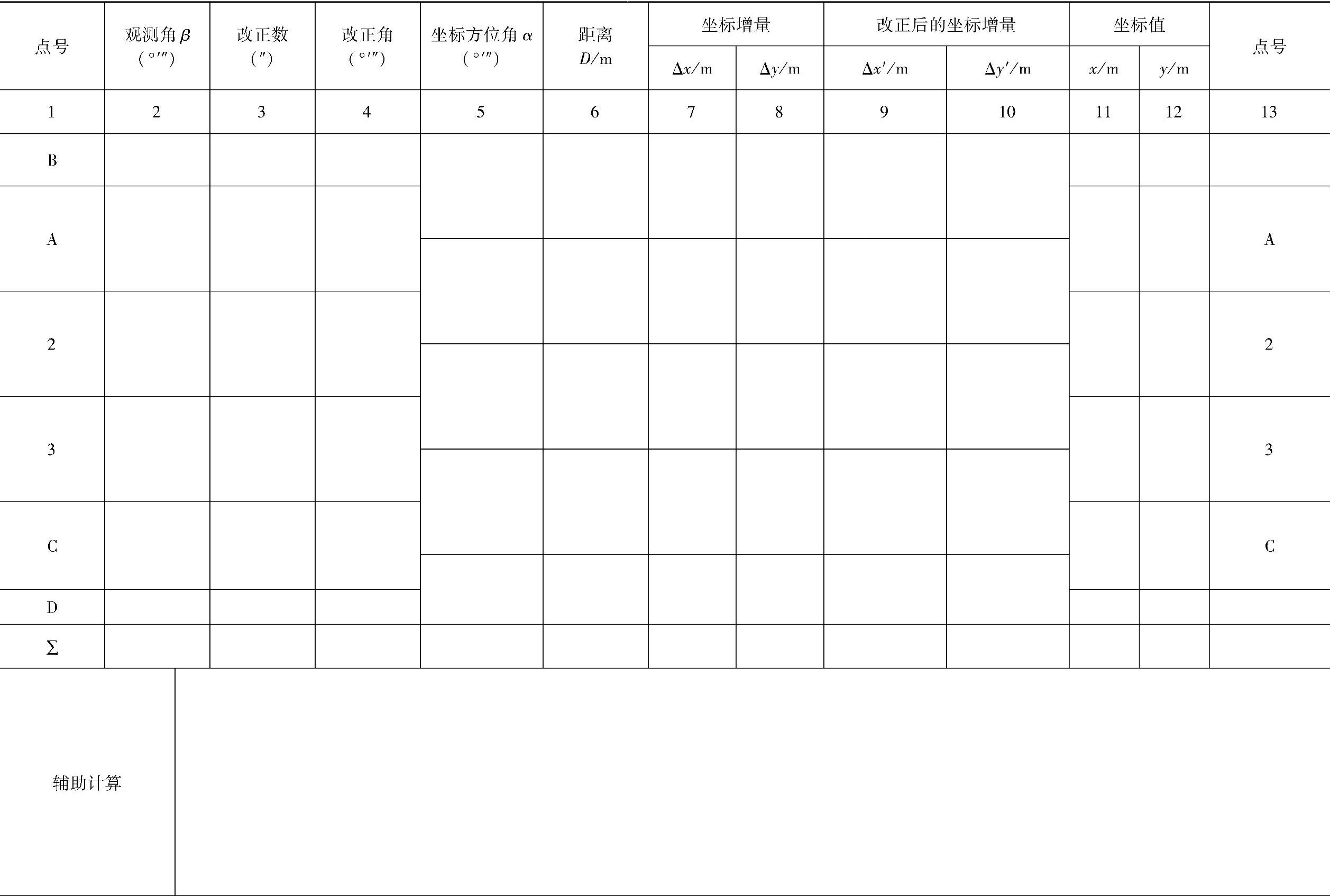
表7-3 符合导线坐标计算表