观测值一般函数的中误差优化

设有函数 Z=f（X₁，X₂，…，X_n） （6-37）

式中 X₁、X₂、…、X_n——独立直接观测值；

ΔX₁、ΔX₂、…、ΔX_n——其相应的真误差，其对应的中误差为m₁、m₂、…、m_n，求函数Z相应的真误差ΔZ。由于自变量含有误差，函数也有误差，其关系式为

Z+ΔZ=f（X₁+ΔX₁，X₂+ΔX₂，…，X_n+ΔX_n）

测量中，由于ΔX_i通常是微小量，ΔX_i可以认为自变量的微分dX_i，故上式可按台劳公式展开成级数，只保留一次幂项，得

Z+ΔZ=f（X₁，X₂，…，X_n）+f/X₁ ΔX₁+f/X₂ ΔX₂+…+f/X_n ΔX_n

由上式减去式（6-37），则得

ΔZ=f/X₁ ΔX₁+f/X₂ ΔX₂+…+f/X_n ΔX_n （6-38）

式中 fX_i——观测值的函数对各观测值X_i的偏导数。

令

f/X₁=K₁，

f/X₂=K₂，

︙

f/X_n=K_n

将其代入式（6-38），即得

ΔZ=K₁ ΔX₁+K₂ ΔX₂+…+K_n ΔX_n （6-39）

这个关系式系线性函数，因此，按公式（6-36），即得

即一般函数的中误差，等于函数对每个直接观测值所求的偏导数与相应观测值中误差乘积的平方和的平方根。式（6-40）是误差传播定律的一般形式，它概括了上述各种形式之函数中误差与观测值中误差的关系。

例6-7 如图6-4所示，设对三角形ABC的两角α、β及γ角所对的边c进行直接观测，观测数据如下。

α=40°10′30″±30″β=80°05′10″±30″

c=350.00m±0.05m。

试求边长a的中误差m_a。

解：计算边长a的函数式为

a=c·sinα/sinγ

由于式中γ系间接观测量，其值按下式算出，即

γ=180°-α-β

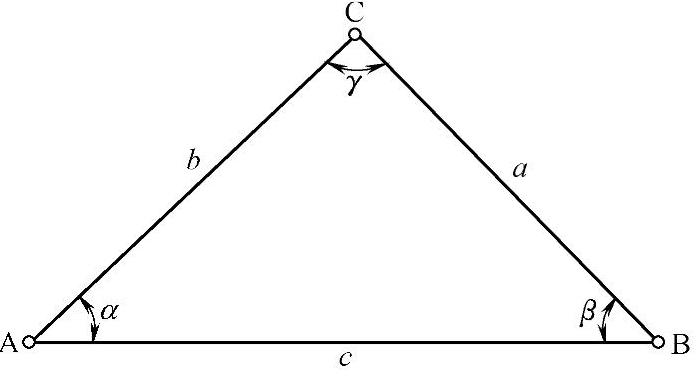
图6-4 求三角形边长的中误差

为求得a边的中误差，可先按式（6-39）写出函数a的微分公式，即(www.xing528.com)

da=a/c·dc+a/α·dα+a/γ·dγ由于角γ系非独立直接观测值，其真误差dγ当然也是非独立真误差，故须用dγ=-dα-dβ来代换，即将dγ代入上式，得

da=a/c·dc+a/α·dα+a/γ（dα-dβ）

注意a边的函数表达式，则有

a/c=sinα/sinγ=a/c

a/α=c/sinγ·cosα=cosα·sinα/sinγ·sinα=acotα

aγ=-c·sinαcosγ/sin²γ=-c·sinα/sinγ·cosγ/sinγ=-acotγ

代入函数的真误差式，得

da=a/c·dc+acotαdα+（acotγ）（-dα-dβ）将上式同类项合并后，得

da=a/c·dc+（acotα+acotγ）dα″/ρ″+acotγdβ″/ρ″

再按公式（6-40）将上式转化为函数的中误差式，即

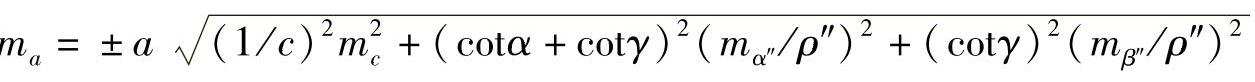
将已知数据代入上式进行计算，求出函数a的中误差m_a。计算中要用到a及γ值，其值为γ=180°-α-β=59°44′20″，a=c·sinα/sinγ=261.414m。则m_a=

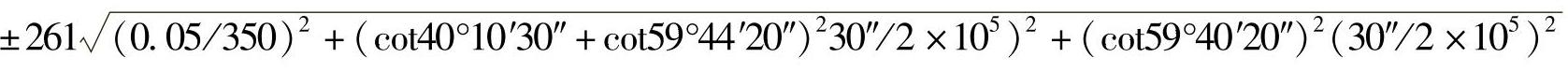
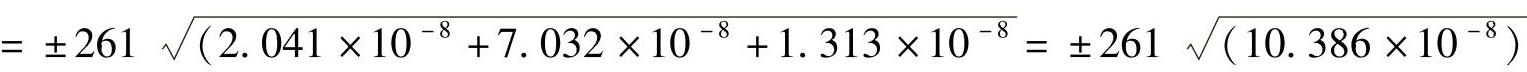
=±261×（3.223×10^-4）=±0.084m

最后结果

a=261.414m±0.084m

综上所述，应用误差传播定律的步骤如下：

（1）列函数式

根据题意中的函数与自变量（直接观测值）的关系，写出相应的函数式

Z=f（x₁，x₂，…，x_n）

（2）求函数真误差的表达式

真误差关系式中的各系数，可通过求各观测值的偏导数得出。但在由真误差关系式转换为中误差关系式之前，必须认真检查真误差关系式中各变量的真误差是否互相独立。若有不独立的情况，应通过误差代换，同类项合并，使所求量的误差表达为独立误差的函数，并注意单位统一，然后才能应用误差传播定律，将其转换成中误差式。

（3）计算函数中误差

将真误差代以相应的中误差，然后将式中的各项各自平方，且在其右边冠以“+”号连接起来，再求平方根，即可得出函数的中误差式，即

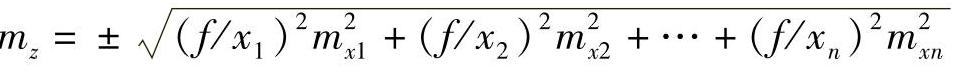
（4）进行具体计算

将各观测值及其相应的中误差代入观测值函数中误差式进行计算。