设有函数
Z=X±Y (6-25)
式中X、Y——直接观测值;
Z——直接观测值X、Y的和或差的函数。
当直接观测值X、Y含有相应的真误差ΔX、ΔY时,函数Z必然也产生真误差ΔZ,则有
Z+ΔZ=(X+ΔX)±(Y+ΔY)
将上式与式(6-25)相减,得ΔZ=ΔX±ΔY (6-26)
这就是和或差函数的观测值真误差与函数真误差之间的关系式。
当对X、Y均独立直接观测n次时,则有
ΔZ1=ΔX1±ΔY1
ΔZ2=ΔX2±ΔY2
︙
ΔZn=ΔXn±ΔYn
将等式两边平方,得
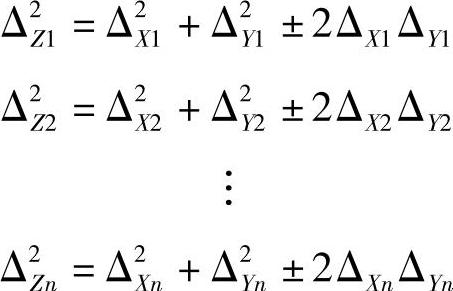
将上列n式相加,并除以观测次数n,得
[Δ2Z]/n=[ΔX2]/n+[Δ2Y]/n±2[ΔXΔY]/n
当n→∞时,等式两边取极限。
limn→∞[Δ2Z]/n=limn→∞[ΔX2]/n+limn→∞[Δ2Y]/n±2limn→∞[ΔXΔY]/n
按中误差定义,得
m2Z=m2X+m2Y±2limn→∞[ΔXΔY]/n (6-27)
上式右边的第三项,由于ΔX、ΔY均为独立直接观测值X、Y的真误差,属于偶然误差性质。根据偶然误差特性ΔXi、ΔYi仍具有偶然误差性质,当n趋近无穷大时,[ΔXΔY]/n将趋近于零,即
limn→∞[ΔXΔY]/n=0 (6-28)
以后将满足上式的误差ΔX、ΔY称为互相独立的误差,简称独立误差,相应的观测值称为独立观测值。在推导误差传播定律的公式时,对于独立观测值来说,式(6-14)可写为
m2Z=m2X+m2Y(https://www.xing528.com)
也即是
由上式可知,两个独立直接观测值之和或差的函数中误差,等于这两个独立直接观测值中误差之平方和的平方根。
设有n个独立直接观测值的函数
Z=X1±X2…±Xn
根据和或差的函数中误差的推导方法,不难证明,其函数中误差式为
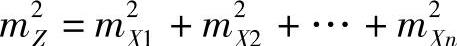
或
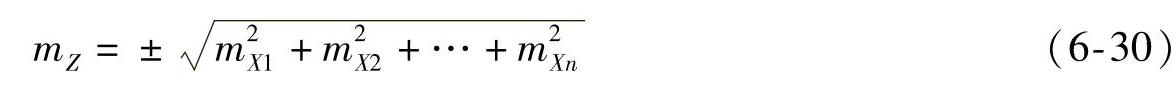
即n个独立直接观测值之和或差的函数中误差,等于各直接独立观测值中误差平方和的平方根。
在特殊情况下,当mX1=mX2=…=mXn=m时,则上式可写为

即n个等精度独立直接观测值的和或差的函数中误差,等于观测值中误差的n倍。
例6-3 在三角形中已测得两角,其中误差分别为±3″和±4″。试根据已测两角的中误差计算出第三角的中误差。
解:按题意得第三角的函数式
C=180°-A-B
则第三角C的中误差,根据式(6-29),可算得
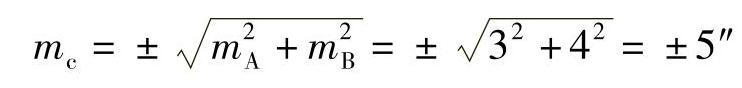
例6-4 如图6-3所示,自水准点A经水准点B、C点向水准点D进行水准测量,观测高差依次为h1、h2、h3,其中误差相应为mh1=±5mm、mh2=±3mm、mh3=±4mm,试求A、D两点间的高差中误差。

图6-3 求高差中误差
解:该题的函数式为
hAD=h1+h2+h3
则其高差hAD的中误差,依式(6-30)可计算得
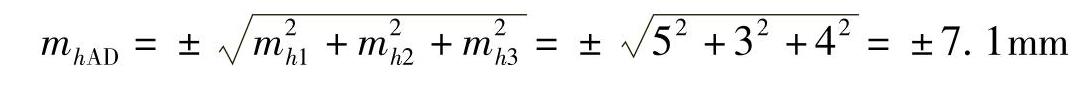
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




