改正观测值中误差的计算方法

一组等精度的观测值在真值已知的情况下（例如三角形的三内角之和），可以按式（6-1）计算观测值的真误差，按式（6-6）计算观测值的中误差。

在一般情况下，观测值的真值X往往是不知道的，真误差Δ也就无法求得，因此就不能用式（6-6）求中误差。由上一节可知，在相同观测条件下对某量进行多次观测，可以计算其最或然值──算术平均值X及各观测值的改正值v_i；并且也知道，最或然值x在观测次数无限增多时，将逐渐趋近于真值X。在观测次数有限时，以x代替X，就相当于以改正值v_i代替真误差Δ_i。由此得到按观测值的改正值计算观测值的中误差的实用公式为

式（6-14）与式（6-6）不同之处：分子以[vv]代替[ΔΔ]，分母以[n-1]代替n。实际上，n和[n-1]是代表两种不同情况下的多余观测数。因为，在真值已知的情况下，所有n次观测均为多余观测，而在真值未知情况下，则其中一个观测值是必要的，其余[n-1]个观测值是多余的。

式（6-14）也可以根据偶然误差的特性来证明。根据式（6-1）和式（6-11）有

Δ₁=X-l₁v₁=x-l₁

Δ₂=X-l₂v₂=x-l₂

︙︙

Δ_n=X-l_nv_n=x-l_n

上列左、右两式分别相减，得到

Δ₁=v₁+（X-x）

Δ₂=v₂+（X-x）(www.xing528.com)

︙

Δ_n=v_n+（X-x） （6-15）

上列各式取其总和，并顾及[v]=0，得到

[Δ]=nX-nx

为了求得[ΔΔ]与[vv]的关系，将式（6-15）等号两端平方，取其总和，并顾及[v]=0，得到

[ΔΔ]=[vv]+n（X-x）² （6-17）

式中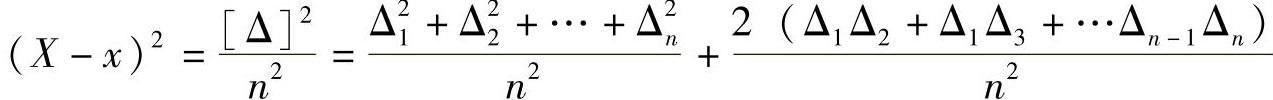，式中右端第二项中Δ_iΔ_j（j≠i）为两个偶然误差的乘积，仍具有偶然误差的特性，根据其第4特性得到

当n为有限数值时，上式的值为一微小量，再除以n后更可以忽略不计，因此

将上式代入式（6-16），得到

由此证明式（6-14）的成立。