偶然误差的特性及优化方法

设某一量的真值为X，对此量进行n次观测，得到的观测值为l₁，l₂……，l_n，在每次观测中发生的偶然误差（又称真误差）为Δ₁，Δ₂……，Δ_n，Δ_n则定义：

Δ_i=X-l_i（i=1，2……，n） （6-1）测量误差理论主要讨论在具有偶然误差的一系列观测值中，如何求得最可靠的结果和评定观测成果的精度。为此，需要对偶然误差的性质作进一步讨论。

就某个偶然误差而言，其符号的正负和数值的大小没有任何规律性。但是，若观测的次数很多，观察其大量的偶然误差，就能发现隐藏在偶然性下面的必然性规律。进行统计的数量越大，规律性就越明显。下面结合某观测实例，用统计方法进行分析。在相同的观测条件下在某一测区共观测了365个三角形的全部内角。由于每个三角形内角之和的真值（180°）已知，因此可以按式（6-1）计算三角形内角之和的偶然误差Δ_i（三角形闭合差），再将正误差、负误差分开，并按其绝对值由小到大进行排列。以误差区间dΔ=2″进行误差个数k的统计，并计算其相对个数k/n（n=365），k/n称为误差出现的频率。结果见表6-1。

按表6-1的数据作图，可以直观地看出偶然误差的分布情况（图6-1）。图中以横坐标表示误差的正负与大小，以纵坐标表示误差出现在各区间的频率（相对个数）除以区间的间隔dΔ，每一区间按纵坐标作成矩形小条，则小条的面积代表误差出现在该区间的频率，而各小条的面积总和等于1。该图称为频率直方图。

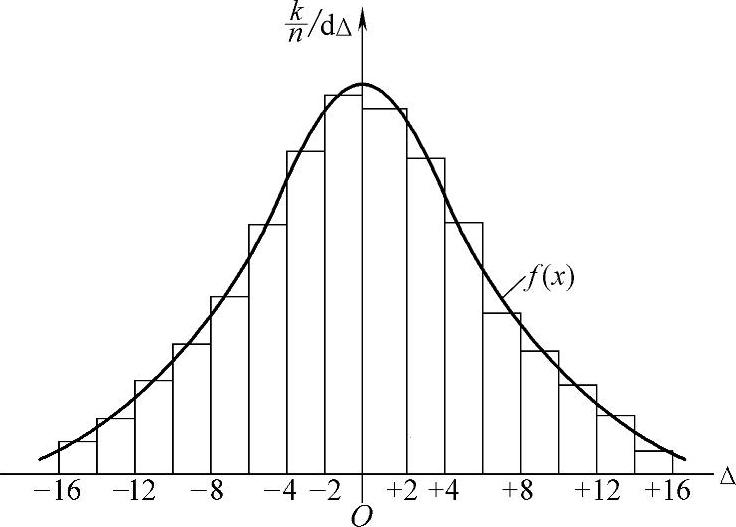
图6-1 频率直方图

表6-1 偶然误差的统计

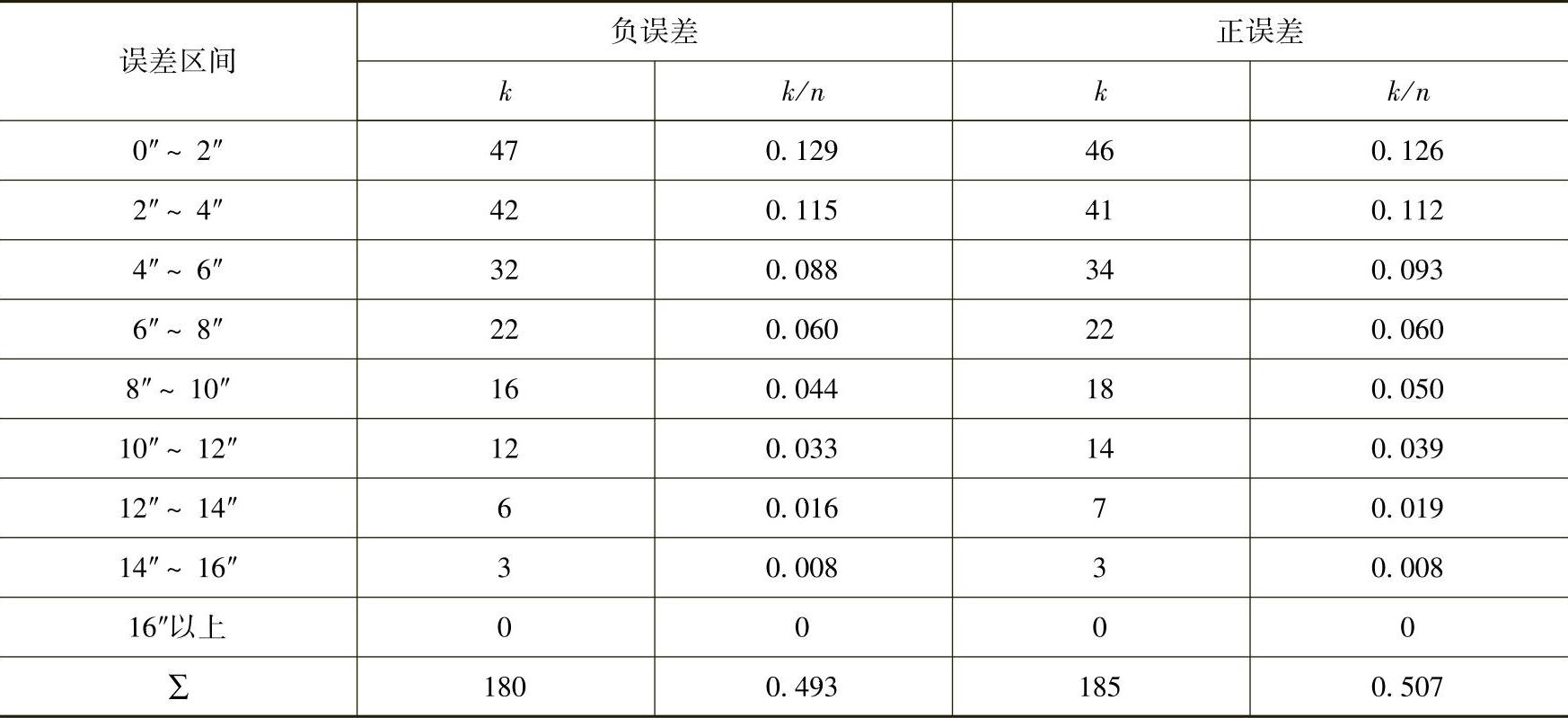
从表6-1的统计中可以归纳出偶然误差的四个特性：

（1）在一定观测条件下的有限次观测中，绝对值超过一定限值的误差出现的频率为零；

（2）绝对值较小的误差出现的频率大，绝对值较大的误差出现的频率小；

（3）绝对值相等的正、负误差出现的频率大致相等；

（4）当观测次数无限增大时，偶然误差的算术平均值趋近于零，即偶然误差具有抵偿性。用公式表示：(www.xing528.com)

式中[]表示取括号中数值的代数和，即[Δ]=Δ₁+Δ₂+…Δ_n；n为Δ的个数。

以上根据365个三角形角度闭合差作出的误差出现频率直方图的基本图形（中间高、两边低并向横轴逐渐逼近的对称图形），并不是一种特例，而是统计偶然误差出现的普通规律，并且可以用数学公式表示。

当误差的个数n→∞，同时又无限缩小误差的区间dΔ，则图6-1中各小长条的顶边的折线就逐渐成为一条光滑的曲线。该曲线在概率论中称为正态分布曲线，它完整地表示了偶然误差出现的概率p（当n→∞时，上述误差区间内误差出现的频率趋于稳定，成为概率）。正态分布的数学方程式为

式中，π=3.1416为圆周率；e=2.7183为自然对数的底；σ为标准差，标准差的平方σ²称为方差。方差为偶然误差平方的理论平均值，为

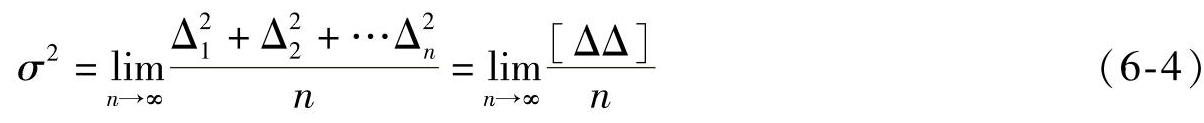
标准差为

由式（6-5）可知，标准差的大小取决于在一定条件下偶然误差出现的绝对值的大小。由于在计算时取各个偶然误差的平方和，当出现有较大绝对值的偶然误差时，在标准差σ中会得到明显的反映。

式（6-3）称为正态分布的密度函数，以偶然误差Δ为自变量，标准差σ为密度函数的唯一参数。