表示直线方向的方法：从基础到实践

通常用方位角和象限角来表示直线的方向。

1.坐标方位角

从标准方向北端起，顺时针方向量到某直线的夹角。用α来表示，角值范围0°～360°。因标准方向的不同又可分为真方位角、磁方位角和坐标方位角。如图4-13所示。

2.正反坐标方位角

一条直线有正反两个方向，通常以直线前进的方向为正方向。由图4-14中可以看出一条直线正反方位角的数值相差180°，即

α_正=α_反±180° （4-13）

图4-13 坐标方位角

3.象限角

测量上有时用象限角来确定直线的方向。所谓象限角，就是由标准方向的北端或南端起量至某直线所夹的锐角，常用R表示，角值范围0°～90°。

4.坐标方位角和象限角的换算关系

坐标方位角和象限角均是表示直线方向的方法，它们之间既有区别又有联系。在实际测量中经常用到它们之间的互换，由图4-15可以推算出它们之间的互换关系，见表4-2所示。(www.xing528.com)

图4-14 正、反坐标方位角

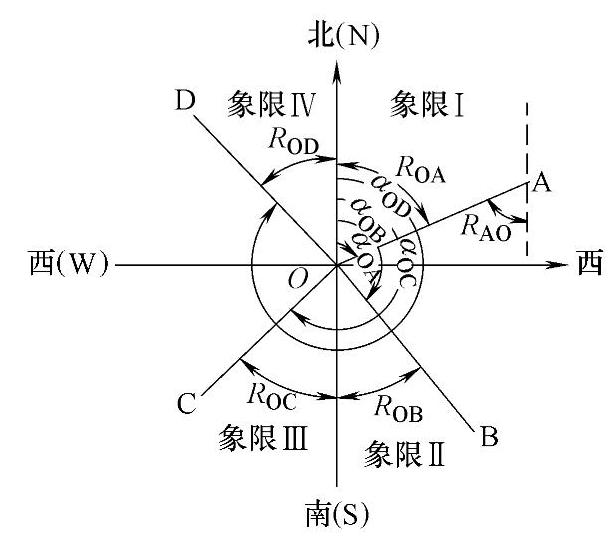
图4-15 坐标方位角与象限角

表4-2 坐标方位角和象限角的换算

【例】某直线AB，已知正坐标方位角α_AB=334°31′48″，试求α_BA、R_AB、R_BA。

解：α_BA=334°31′48″-180°=154°31′48″

R_AB=360°-334°31′48″=25°28′12″NW

R_BA=180°-154°31′48″=25°28′12″SE