电路的波特图及其应用

在研究一些电路的频率响应时，输入信号的频率范围常常需要设置得很宽，不方便对频率轴使用线性标度，因此在绘制频率特性曲线时，常常采用对数坐标，称为波特图。

波特图由对数幅频特性和对数相频特性两部分组成。采用对数坐标系，横轴为lgf（即横轴以每10倍频点画），可开阔视野；幅频特性纵轴为20lg，单位为“分贝”（dB），相频特性纵轴仍然用φ来表示，这使得原计算式中的乘法运算变成了加法运算。波特图的传递函数的半对数图已经成为行业标准。

在电路的近似分析中，为简单起见，常将波特图的曲线折线化，图9－10所示为高通电路波特图，图9－11所示为低通频率特性的波特图，fH和fL分别称为上限截止频率和下限截止频率，截止频率取决于电容所在回路的时间常数τ，当信号频率等于fH和fL时，幅频特性曲线下降到中频的0.707倍，即下降3dB。

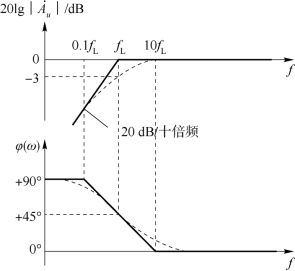
图9－10　高通电路波特图

图9－11　低通电路波特图(www.xing528.com)

全频域放大倍数表达式如式（9－3）所示，全频域波特图如图9－12所示，fH－fL称为通频带，一般用符号BW表示，有关通频带在9.2.3小节中有详细的描述。称为通带放大倍数，通带放大倍数定义为通带中输出电压与输入电压的比值；下降到0.707倍时对应的频率称为通带截止频率；从通带截止频率到接近0的频率为过渡带，由图可见，过渡带f每下降10倍，幅频特性曲线放大倍数变化20dB，即对数幅频特性在过渡带可以等效成斜率为20dB/十倍频或－20dB/十倍频的直线。过渡带越窄，电路的选择性越好，滤波特性越理想。分析滤波电路主要是求解通带放大倍数、通带截止频率和过渡带的斜率。

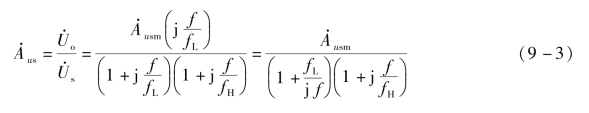
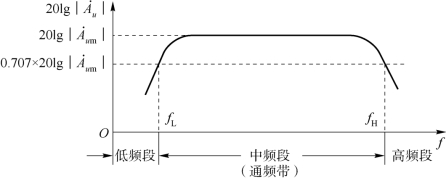
图9－12　全频域波特图

课后思考

（1）为什么要把RC低通滤波器的截止频率定义为当幅度下降到最大值的时的频率，而不是定义在幅度下降到最大值的黄金分割点0.618的位置呢？

（2）为回答第一个思考题，请读者计算，在对应的截止频率处，负载得到的功率是ω＝0时功率的多少倍？若截止频率定义在对应处，负载得到的功率又是ω＝0时功率的多少倍？