T形异名端共端去耦等效方法

图8－15所示的电路是异名端为共端的T形连接。根据所标电压、电流的参考方向及KCL，得

图8－14　同名端共端的T形去耦等效电路

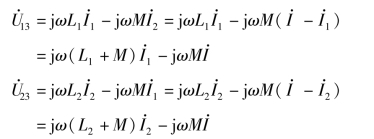
由上述方程可得图8－16所示的无互感等效电路。通过等效变换，用T形等效电路代替原来的电路后，就不必再考虑互感M，这种方法称为互感消去法。

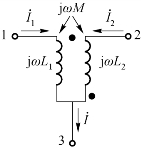
图8－15　T形连接

（异名端共端）

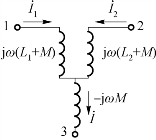
图8－16　异名端共端的T形去耦等效电路

在使用互感消去法时，如果将L1和L2等效替代的电感记为和，而把另外等效出的电感记为L3，则T形去耦等效电路中3条支路的等效电感分别如下。

支路1：＝L1∓M（同侧为“－”，异侧为“＋”）；

支路2：L2＝L2∓M（同侧为“－”，异侧为“＋”）；

支路3：＝±M（同侧取“＋”，异侧取“－”）。

例8－4　求图8－17（a）和图8－17（b）所示电路的等效电感Lab。

解题步骤如下。

（1）分析图8－17（a）中4H和6H电感为T形结构，应用T形去耦等效电路得图8－18（a）所示电路。则等效电感为

(www.xing528.com)

（2）分析图8－17（b）中5H和6H电感为同侧相接的T形结构，2H和3H电感为异侧相接的T形结构，应用T形去耦等效电路得图图8－18（b）所示电路。则等效电感为

图8－17　例8－4题图

图8－18　例8－4解图

例8－5　求图8－19所示电路的端口复阻抗Zab。

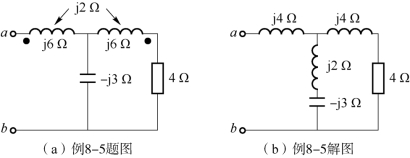
图8－19　例8－5图

求解步解：图8－19（a）中的电感为同侧相接的T形结构，求两个电感的T形等效，则有

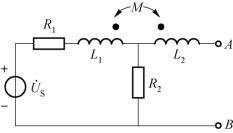
图8－20　练一练题图

知识点归纳

（1）把互感耦合电路等效变换成无耦合的电路，称为去耦。

（2）当同名端顺向串联时：Leq＝L1＋L2＋2M；当同名端反向串联时：Leq＝L1＋L2－2M。

（3）当同名端同侧并联时：；当同名端异侧并联时：

（4）当耦合电感的两个线圈各取一端连接起来与第三条支路形成一个仅含3条支路的共同节点，称为耦合电感的T形连接。若两个线圈同名端相连，则T形去耦等效出3个电感分别为L1－M、L2－M和M；若两个线圈异名端相连，则T形去耦等效出的3个电感分别为L1＋M、L2＋M和－M。