分析计算三相电路功率

1.三相电路的功率

在三相交流电路中，无论三相负载对称与否、是星形连接还是三角形连接，其每一相负载功率的计算方法与单相交流电路是完全相同的，而三相电路总的有功功率一般情况下等于各相负载有功功率之和，即

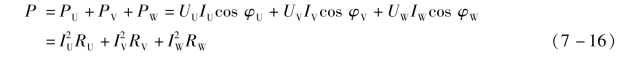
式中　UU，UV，UW——各相相电压；

　　　IU，IV，IW——各相相电流；

　　　cosφU，cosφV，cosφW——各相电路的功率因数。

同理，三相电路的总无功功率等于各相负载无功功率之和，即

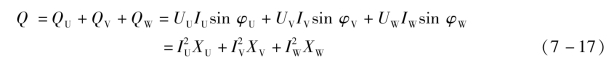
三相电路总的视在功率为

应该注意，在计算三相电路总视在功率时，假若三相电路为不对称负载，虽然三相电压对称，但三相负载电流是不对称的，此时有

因此，一般情况下，计算三相电路总的视在功率不能像计算三相电路总有功功率那样，用求代数和的方法。

三相电路总的功率因数为

2.对称三相电路的功率

若三相负载是对称的，由于每相功率都相等，则可用相电压、相电流计算三相电路总的有功功率，即

式中　UP，IP——负载上的相电压和相电流。

当负载为星形连接时，有

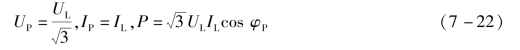
当负载为三角形连接时，有

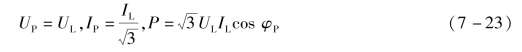
由式（7－22）和式（7－23）可看出，对称三相电路总的有功功率计算公式为

与负载的连接方式无关。但应注意，φP由负载的阻抗角决定，它仍然是相电压与相电流之间的相位差，而不是线电压与线电流的相位差。

实际上，由于测量三相负载电路中的线电压和线电流比测量相电压、相电流容易，因此，在三相电路负载对称时，用线电压、线电流计算三相电路的总功率更具有实用意义。

同理，若三相负载对称，则无论负载接成星形还是三角形，都有

(www.xing528.com)

而对称三相电路总的视在功率为

对称三相负载总的功率因数为

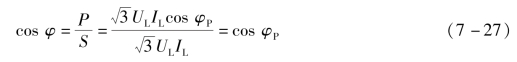
式中　cosφP——每相负载的功率因数。

上式表明，在对称情况下，三相负载总的功率因数就是每相负载的功率因数。在不对称负载中，各相功率因数不同，三相负载的功率因数值无实际意义。

例7－11　有一台异步交流电动机，其每相绕组的复阻抗Z＝80＋j60Ω，对称三相电源线电压UL＝380V。求当电动机三相绕组分别连接成星形和三角形时电路的有功功率、无功功率、视在功率和功率因数。

电路分析：由于异步交流电动机是对称三相负载，与对称三相电源构成的是对称三相电路，因而可以先计算不同连接方式下的电压和电流，然后利用对称三相电路功率公式直接对各功率进行计算。

解：由于是对称三相电路，电动机总的功率因数为每相绕组的功率因数，即

由上题分析可以看出，在电源线电压一定时，异步电动机三相绕组作Y连接时的线电流是△连接时线电流的1/3，即可以减少启动电流，而作△连接时的功率是Y连接时功率的3倍，可以提高异步电动机正常运行时的输出功率，这就是异步电动机启动时采用Y连接，而正常运行时通常采用△连接的原因。

例7－12　已知三相电路连接的负载如图7－29所示，阻抗Z1＝30＋j40Ω，电动机负载的功率P＝1700W，电路线电压UL＝380V，cosφ＝0.8（感性）。求线电流和电源发出的总功率。

电路分析：由于该电路连接有两相对称负载，可以分别计算每相负载的电流，然后计算总电流，而电源发出的总功率为电路总的有功功率，因而最后可以利用电路总的有功功率公式进行计算。

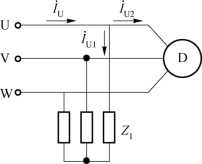
图7－29　三相电路负载连接

解：（1）设电源电压

当然对于例7－12中的多组负载电路，也可以分别计算每组负载的有功功率，然后将各负载功率相加就是电路总的有功功率。

3.对称三相电路的瞬时功率

设对称三相电路U相负载瞬时电压为uU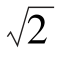＝Usin（ωt），电流为iU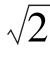＝Isin（ωt－φ）则U相负载瞬时功率为

同理，可得其他两相负载瞬时功率为

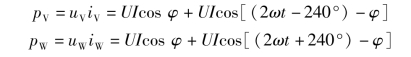
而三相电路总瞬时功率为各相瞬时功率之和，即

由于cos（2ωt－φ）＋cos（2ωt－240°－φ）＋cos（2ωt＋240°－φ）＝0因而可进一步推得三相电路总的瞬时功率为

式（7－28）表明，对称三相电路的瞬时功率是一个常量，其值等于平均功率，这是对称三相电路的优点之一，反映在三相电动机上，就得到均衡的电磁力矩，避免了机械振动，这是单相电动机所不具有的。