相量法分析正弦交流电路的方法及应用

在正弦交流电路中只要正弦电源都是同频率，且构成电路的电阻、电感、电容元件都是线性的，则不仅直流电路中的欧姆定律、基尔霍夫定律能以相量形式适用于正弦交流电路，其他所有在直流电路中讨论过的网络分析法、原理和定理等也都完全适用。

将直流电路中的电阻用复阻抗替代，电导用复导纳替代，所有正弦量都用相量表示，就可以实现相量法分析线性正弦交流电路。

1.网孔电流法

如图6－32所示，若图中的电压相量及容抗XC、感抗XL和电阻都已知，则可以设定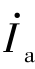、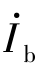为两个网孔的网孔电流。对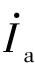绕行的网孔而言，其自阻抗就是R－jXC；对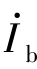绕行的网孔而言，它的自阻抗为R＋jXL。电阻R则是两个网孔的互阻抗。与直流分析相同，自阻抗总取正值。互阻抗则因设定的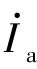、两网孔电流在互阻R上的方向不一致，因此取负。电源电压也按是否与网孔电流方向一致取负号或正号。因此就有网孔方程组，即

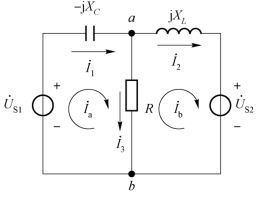
图6－32　正弦交流的网孔电流法

（例6－20和例6－21电路图）

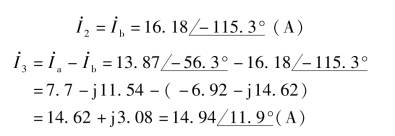
2.节点电压法

用相量形式的节点电压法也可对电路进行求解。

例6－21　试用节点电压法求例6－20中图6－32中各支路的电流。

解题思路如下。

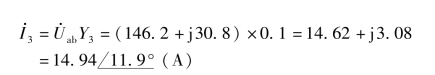
3.戴维南定理

求正弦交流电路中某一条支路上的电流，同样可用戴维南定理求解。比如，求解图6－33（a）中流过电阻R2上的电流，就可以将其视作一个线性含源二端网络连接了电阻R2的支路。(www.xing528.com)

将图6－33（a）所示电路中的R2支路断开，可求得该线性含源二端网络的开路电压，即

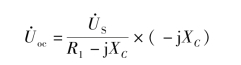
把该二端网络内的电源置零，则端口等效复阻抗为

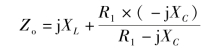
随后就可以将该二端网络等效成一个电压为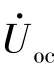的电源与复阻抗Zo串联，如图6－33（b）中虚线框所示。将这个等效二端电路连回R2支路，就可求得R2支路上的电流。

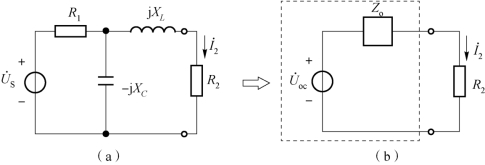
图6－33　正弦交流电路的戴维南定理

练一练：

试用戴维南定理求解图6－32中电阻R上的电流。

（1）整理电路，使电路为一个含源二端网络与R支路相连。

（2）移开R支路，求端口电压：_________________________________。

（3）再求入端复阻抗：_________________________________________。

（4）得出等效电路后连回R支路，求流过R的电流：______________。

解题微课