复阻抗和复导纳的等效变换方法

复导纳与复阻抗等效变换即利用两者互为倒数的关系。前文通过例6－15已印证并归纳了复阻抗模与复导纳模，以及阻抗角φ与导纳角φy之间分别满足

若设复阻抗Z＝R＋jX与复导纳Y＝G＋jB等效，则根据两者定义，就相当于一个电阻与一个电抗的串联电路等效成一个电导与一个电纳的并联，如图6－30所示。

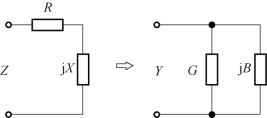
图6－30　复阻抗与复导纳的等效变换

在实际应用中，往往在得出等效复阻抗或复导纳后，再利用电导与电阻之间、感纳与感抗之间，以及容纳与容抗之间的倒数关系，获得等效的R、L、C参数。

例6－19　RL串联电路如图6－31（a）所示，已知R＝50Ω、L＝0.06mH。求在ω＝106rad/s时，等效并联电路图6－31（b）中的R′和L′。

解题步骤如下。

（1）计算图6－31（a）中的感抗，有

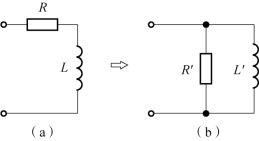
图6－31　例6－19电路图

（2）写出图6－31（a）中的复阻抗，有(www.xing528.com)

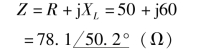
（3）计算图6－31（a）中的等效复导纳，有

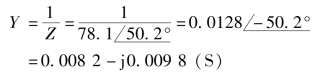
由该式可知，等效复导纳可视作一个G＝0.0082S的电导和一个B＝－j0.0098S的电纳并联。通过Y＝G＋j（BC－BL）可进一步确定该电纳就是一个感纳BL。

（4）根据电导与电阻之间、感纳与感抗之间的倒数关系，得图6－31（b）中的等效参数，即

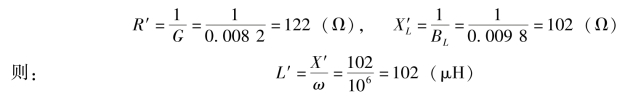
知识点归纳

（1）多个复阻抗串联，等效复阻抗Z＝Z1＋Z2＋Z3＋…＋Zn。

（2）多个复阻抗并联，等效复阻抗的倒数当仅有两个复阻抗并联时，等效复阻抗

（3）多个复阻抗并联也可视作多个复导纳并联，等效复导纳Y＝Y1＋Y2＋Y3＋…＋Yn。

（4）一个电阻与一个电抗的串联，即Z＝R＋jX，可以等效成一个电导与一个电纳的并联，即Y＝G＋jB。两者的等效关系满足

（5）复阻抗与复导纳互为倒数关系。其含义包括：

复阻抗模与复导纳模之间有阻抗角φ与导纳角φy之间有φ＝－φy。