复阻抗和复导纳的并联与串联

1.复阻抗的串联

例6－16　图6－26（a）所示的无源二端网络有两个负载，Z1＝5＋j5Ω和Z2＝6－j8Ω相串联，接外部正弦电压u＝220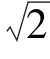sin（ωt＋30°）V。求该二端网络对外的等效复阻抗Z、两负载上的电压和电流i。

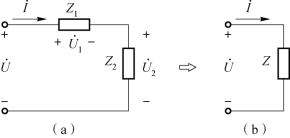
图6－26　例6－16电路图（复阻抗串联）

解题思路如下。

两个复阻抗串联，则Z1上的电压为，Z2上的电压为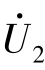，根据KVL的相量形式，有

可见，两个复阻抗串联，可以等效成一个复阻抗，如图6－26（b）所示。该等效复阻抗为两复阻抗之和，即

不难证明，当多个复阻抗Z1、Z2、Z3、…、Zn串联时，等效复阻抗等于各复阻抗之和，即

通过该分析，该题即能求解。

解题步骤如下。

2.复导纳的并联

图6－27（a）所示为两个复导纳并联，则流过Y1的电流为，流过Y2的电流为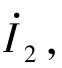根据KCL的相量形式，有

可见，两复导纳并联后可等效成一个导纳Y，如图6－27（b）所示。等效导纳的数值是Y＝Y1＋Y2。

不难证明，当多个复导纳Y1、Y2、Y3、…、Yn并联时，等效复导纳等于各复导纳之和，即

由于导纳是阻抗的倒数，因此式（6－51）也可以写成

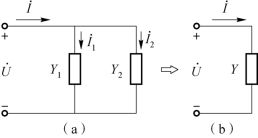
图6－27　复导纳并联(www.xing528.com)

对两个并联的阻抗而言，经过式（6－52）的换算，可得

式（6－53）与两电阻并联方法类似。可以进一步证明，复阻抗的串、并联计算及分压、分流计算，都与电阻的计算方法相同，只是在正弦交流激励下，计算都采用相量法。

例6－17　一个无源二端网络由两个负载并联。一个负载是电阻为3Ω、感抗XL为4 Ω的电感线圈，另一个负载由一个8Ω的电阻与容抗XC为6Ω的电容器串联构成。两负载并联后接外部正弦电压u＝220sin（ωt＋10°）V。求该二端网络对外的等效复导纳、电路端口上的总电流。

解题思路如下。

该题有多种解题方法，两个复阻抗的并联最常见的是利用式（6－53）计算出等效复阻抗，它的倒数就是等效复导纳。随后可用相量形式的欧姆定律，获得端口电流·I。

也可直接用复导纳并联的方法求解（读者可用不同的方法互相验证）。

解题步骤如下。

练一练：

已知一个二端网络如图6－28所示，R1＝30Ω、R2＝100Ω，L＝1mH，C＝0.1μF。在ω＝105rad/s时，求该电路的端口等效阻抗Z。

图6－28　练一练题图

解题微课

例6－18　图6－29所示电路是音频信号发生器中常用的选频电路。选频是指当这个二端网络的输入电源u1为某一频率时，u2电压能达到最大值，且同相。已知R、C，试用等效阻抗的方法确定的比值以及同相的条件。

解题步骤如下。

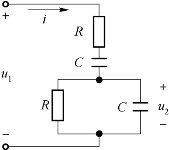
图6－29　例6－18电路

（应用电路：选频网络）

通过该例题，可知选频网络输入及输出电压同相且输出达到最大值的条件是R＝XC。由于，因此可得获取这一条件的端口输入电压频率为