串并联阻抗与导纳分析

相量形式的欧姆定律不仅对单一的分立元件适用，对多个元件的组合也同样适用。图6－18（a）是一个由多个元件构成的无源线性二端网络。当它在角频率为ω的正弦电源激励下处于稳定状态时，端口的电压相量和电流相量的比值就是该端口的阻抗Z，定义为

其中的称为阻抗模，φ＝φu－φi称为阻抗角。这样图6－18（a）所示的无源二端网络就可以等效成图6－18（b）所示的电路，所以Z也称为无源二端网络的等效阻抗或输入阻抗。

图6－18　无源线性二端网络与等效电路

当这一阻抗是纯电阻时，Z＝R，是纯实数；当这一阻抗是纯电感或者纯电容时，Z＝jXL或Z＝－jXC，是纯虚数。

1.RLC串联电路

例6－14　一个RLC串联电路如图6－19（a）所示。电阻R＝4Ω，电感L＝19.11mH，电容C＝1062μF，该电路中通过的电流为i＝10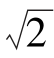sin314tA。求：（1）电路的总电压；（2）各元件上的分电压；（3）绘出电压和电流的相量图。

图6－19　例6－14电路图（RLC串联）

解题思路：

一个RLC串联电路，已知流过的电流为i＝Isinωt的形式，则该电路是一个正弦交流响应电路。当电压u与电流i取关联参考方向时，按照瞬时值表达的电压关系，则总电压有

式（6－40）是传统的微积分方程，尽管通过解方程也能求出总电压和各元件上的分电压，但很烦琐。

学习了相量法以后，就可以将图6－19（a）转换成图6－19（b）的形式，依照相量形式的基尔霍夫电压定律，有

式（6－41）中复数的虚数部分X称为电抗，X＝XL－XC，式中的Z＝R＋jX。Z是一个复数，因此也称为复阻抗。图6－19（b）所示电路的复阻抗可归纳为

其中的复阻抗模为

阻抗角为

通过上述分析，可以按相量法进行解题。

解题步骤如下。

（1）以电流为参考相量，写出电流相量式：

（2）计算感抗：XL＝ωL＝314×19.11×10－3＝6（Ω）

（7）画出相量图如图6－20所示。

图6－20　例6－14相量图

由于是串联电路，因此将电压三角形中的所有相量同除以电流的有效值，可得图6－21中的阻抗三角形。同理有

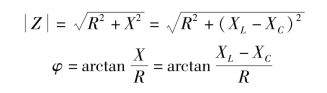
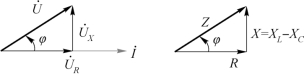
图6－21　电压三角形与阻抗三角形

此处得出的结论与式（6－43）一致。

例6－14中的总电压超前总电流36.9°，说明该电路对外呈电感性的特征。

在RLC串联正弦交流电路中，根据相量图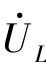和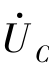的大小，可分为3种情况，即UL＞UC、UL＜UC和UL＝UC。

①当UL＞UC时，UL－UC＞0，即两者的矢量和＋为正，如图6－22（a）所示。此时阻抗角φ＞0，总电压超前总电流。此时电抗X＝XL－XC＞0，电路对外呈感性。

②当UL＜UC时，UL－UC＜0，即两者的矢量和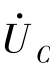＋为负，如图6－22（b）所示。此时阻抗角φ＜0，总电压滞后总电流。此时电抗X＝XL－XC＜0，电路对外呈容性。

③当UL＝UC时，两者的矢量和＋为零，如图6－22（c）所示。此时阻抗角φ＝0，总电压与总电流同相。此时电抗X＝XL－XC＝0，电路对外呈阻性。

图6－22　RLC串联电路的相量图

从上述电路的解题过程可以总结出RLC串联电路求解的一般步骤如下。

（1）求出电路中的各个阻抗参数。

（2）当电路中有多个电感和电容时，需对电感和电容分别进行等效计算。

（3）复阻抗Z的实部R是串联电路中的等效电阻部分；虚部X是感抗和容抗的代数和，运算时感抗取正、容抗取负。

（4）已知电路电流时，以电流为参考相量，求出各元件上的电压和总电压的相量式，再写出各电压的解析式。

（5）若已知电源电压时，则以电压为参考相量，先求电路中的电流，再求各元件上的电压，最后根据解得的相量式，写出电流及各电压的解析式。

练一练：

一个RLC串联电路的电阻R＝30Ω，感抗XL＝100Ω，容抗XC＝60Ω。该电路外加电压u＝220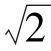sin（314t）V。试求：电路的总阻抗Z、总电流I和i的瞬时解析表达式，并且说明该电路对外呈电感性还是电容性。(www.xing528.com)

解题微课

（1）计算复阻抗：_____________________________________________。

（2）写出总电压的相量并计算总电流的相量式：___________________。

（3）写出电流i的解析式：_____________________________________。

（4）判断电路的性质并给出判断依据：___________________________。

2.RLC并联电路

例6－15　一个RLC并联电路如图6－23所示。电阻R＝20Ω，电感L＝50mH，电容C＝80μF，加在该电路两端的电压为u＝110sin314tV。求：（1）电路的总电流；（2）各元件上的分电流；（3）绘出电压和电流的相量图。

解题思路如下。

一个RLC并联电路，已知施加的电压为u＝Usinωt的形式，则该电路是正弦交流响应电路。当电压u与电流i取关联参考方向时，按照瞬时值表达的电流关系，则总电流有

图6－23　例6－15电路图（RLC并联）

解式（6－45）这样的微积分方程，也很烦琐。

将电路参数换成相量形式，依照相量形式的KCL，有

通过上述分析，可以用导纳法进行解题。

解题步骤（导纳法）如下。

（7）画出相量图，如图6－24所示。

图6－24　例6－15相量图

由于是并联电路，因此将电流三角形中的所有相量同除以电压的有效值，可得图6－25中的导纳三角形。通过导纳三角形可得出与式（6－48）一致的结论。

图6－25　电流三角形与导纳三角形

例6－15也可以用阻抗法求解。

解题步骤（阻抗法）如下。

根据相量式画相量图，并写出各电流的解析式。此处省略。

比较导纳法和阻抗法，尽管在只有单个电容、电感的情况下，两种方法看不出太大区别，但当并联电路中有多个电容、电感及电阻时，导纳法就相对而言更为简便。

在应用时，技术人员一般根据实际电路情况及已知条件，选择导纳法或阻抗法。

②阻抗角φ与导纳角φy的关系是：φ＝－φy。

从上述电路的解题过程可以总结出RLC并联电路求解的一般步骤为：

（1）求出电路中的各个导纳参数。

（2）当电路中有多个电感和电容时，需对电感和电容分别进行等效计算。

（3）复导纳Y的实部G是并联电路中的等效电导部分；虚部B是感纳和容纳的代数和，运算时容纳取正、感纳取负。

（4）并联电路一般以总电压为参考相量，求出各元件上的电流和总电流的相量式，再写出各电流的解析式。

（5）若已知总电流，则通过复导纳（或复阻抗）先求出电路中的总电压（即各元件并联端的电压）；再求流过各元件的电流；最后根据解得的相量式，写出电压及各电流的解析式。

练一练：

一个RLC并联电路外加电压u＝220sinωtV，电阻R＝27.5Ω，感抗XL＝22Ω，容抗XC＝55Ω。试求：

（1）求各支路电流：___________________________________________。

（2）求总电流：_______________________________________________。

（3）绘出相量图：_____________________________________________。

（4）计算复阻抗和复导纳：_____________________________________。

解题微课

知识点归纳