分立元件的阻抗和导纳分析

如前文所述，线性电路在同一频率的正弦激励下，电路全部的稳态响应也将是同一频率的正弦函数。这类电路泛称正弦稳态交流电路。在这类电路中，电阻元件、电感元件和电容元件上的电压和电流也都是同频率的正弦波。掌握这3种基本元件上正弦量的相量形式，是进一步用相量法分析正弦稳态电路的基础。

1.3种基本元件伏安关系的相量形式

1）纯电阻电路

纯电阻电路是只有电阻负载的交流电路，常见的荧光灯、电烙铁等交流电路都是纯电阻交流电路。

如图6－9所示，设通过电阻R的电流为则该电阻两端的电压依据欧姆定律为

根据式（6－24）可知，电阻上的电压和电流是同频率、同相位的关系。用波形图表示电压－电流关系如图6－10（a）所示。

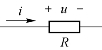
图6－9　流过正弦电流的电阻

图6－10　纯电阻正弦交流电路的波形图和相量图

用相量法表示该电流和电压，则电流相量，电压的相量根据式（6－24）得出。再将电流相量代入，则可以写成

该式表达了电阻上电压和电流之间的相量关系，即在数值上，符合欧姆定律U＝RI，在相位上，电阻上的电压与电流同相。电流和电压的相量图如图6－10（b）所示。

例6－11　纯电阻电路中，电阻为22kΩ，交流电压u＝311sin（314t＋30°）V，求通过电阻的电流多大？写出电流的函数解析式，并画出电阻上电压和电流的相量图。

解题步骤如下。

图6－11　例6－11相量图

图6－12　流过正弦电流的电感

从式（6－26）可知，电感施加正弦交流电以后，电感上的电压与电流同频率、但不同相。电感上的电压超前电流90°。用波形图表示电压－电流关系如图6－13（a）所示。

图6－13　纯电感正弦交流电路的波形图和相量图

式（6－27）表明，电感元件上的电压与电流的有效值关系是U＝ωLI，相位关系是电感上的电压超前电流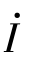为90°。电感上电流和电压的相量图如图6－13（b）所示。

进一步用一个物理量XL来表征电感元件对交流电流的阻碍作用，则有

XL称为感抗，单位为Ω。式（6－28）表明，角频率ω越大，感抗越大。对直流电而言，ω＝0，此时感抗XL＝0，因此电感对直流电相当于短路。

用感抗这一物理量，则式（6－27）也可写为

例6－12　一个电阻可忽略的纯电感电路，电感线圈L＝127mH，接在正弦交流电压为u＝311sin（314t＋30°）V的电源上。求：（1）感抗；（2）写出电压及电流的相量式，并绘出它们的相量图；（3）流过电感的电流解析式。

解题步骤如下。

（1）计算感抗：XL＝ωL＝314×127×10－3＝40（Ω）。

（2）写出电压的相量式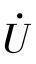：＝22030°（V）。

（3）用相量法计算电流：

（4）绘出相量图如图6－14所示。

图6－14　例6－12相量图

（5）写出电流的函数解析式为

练一练：

一个电感量为0.1H的电感线圈，分别接到电压为u1＝100sin（100t）V和u2＝100sin（1000t）V交流电路中。（1）试分别求出在两个电压下的工作电流；（2）从结果可归纳出什么结论？

（1）求出电感在两个不同角频率下的感抗XL1和XL2：_______________。

（2）用相量法求电流和：__________________________________。

（3）写出两个电流的解析式：___________________________________。

（4）结论归纳：_______________________________________________。

3）纯电容电路

解题微课(www.xing528.com)

如图6－15所示，设一个电容元件C外接的正弦交流电压为u＝Usinωt，则流过电容的电流为

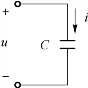
图6－15　外接正弦电压的电容

从式（6－30）可知，电容外接正弦交流电以后，电容上的电压与电流也不同相。电容上的电流超前电压90°。用波形图表示电压－电流关系，如图6－16（a）所示。

图6－16　纯电容正弦交流电路的波形图和相量图

式（6－31）中的－j表示将复平面上的电流相量沿顺时针方向旋转90°，可得电压相量的位置，如图6－16（b）所示。式（6－31）表明，电容元件上的电压与电流的有效值关系是，相位关系是电容上的电流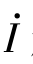超前电压为90°。

进一步用物理量XC来表征电容器在充、放电时对交流电流的阻碍作用，则有

XC称为容抗，单位为Ω。式（6－32）表明，角频率ω越大，容抗越小。对直流电而言，ω＝0，此时容抗XC→∞，因此电容对直流电相当于开路。

用容抗这一物理量，则式（6－31）也可写为

例6－13　一个C＝63μF的电容器接到、频率f＝50Hz的电源上。求：（1）容抗；（2）写出电容器上电流的相量式，并绘出电压和电流的相量图；（3）写出电流的解析式。

解题步骤如下。

（1）计算容抗，即

（2）用相量法计算电流，即

（3）绘出相量图如图6－17所示。

图6－17　例6－13相量图

（4）写出电流的函数解析式：i＝4.4sin（314t＋135°）A。

练一练：

流过50μF电容器的电流i＝100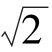sin（300t＋60°）mA。试求电容两端的电压u，并绘出相量图。

（1）求出电容的容抗XC：______________________________________。

（2）用相量法求电压：________________________________________。

（3）写出电压的解析式：_______________________________________。

（4）画相量图。

解题微课

2.3种基本元件的阻抗和导纳

电阻、电感和电容元件在关联参考方向下，它们的伏安关系及相量式分别为

如果把元件在正弦稳态时电压相量与电流相量之比定义为该元件的阻抗，记为Z，则3种基本元件的相量关系都可以归结为

这就是相量形式的欧姆定律。对电阻、电感和电容元件而言，它们的阻抗分别为

它们阻抗的单位都是欧姆（Ω）。

阻抗的倒数定义为导纳，记为Y，则有

结合式（6－34），元件的相量关系也可以归结为

根据式（6－35）的定义，电阻、电感和电容的导纳分别为

由于电感的阻抗就是感抗XL，电容的阻抗就是容抗XC。将感抗的倒数称为感纳，专门记为BL，则有

将容抗的倒数称为容纳，专门记为BC，则有

感纳、容纳等所有导纳的单位都是西门子（S）。