基尔霍夫定律的相量形式解析

一个正弦量可以用函数解析式来描述，也可以用波形图来描述。如果在一个并联电路中存在两条支路，两条支路上的电流分别为i1＝Im1sin（ωt＋φ1）和i2＝Im2sin（ωt＋φ2）。如何求解该电路的总电流i？

众所周知，交流电路的电流、电压的瞬时值也受基尔霍夫定律约束。假设这两个电流的参考方向一致，则总电流i＝i1＋i2＝Im1sin（ωt＋φ1）＋Im2sin（ωt＋φ2）。不难看出，如果用波形图来求解，就需要把两电流在各时刻的瞬时值逐点相加，十分烦琐。如果采用函数法，则要利用三角函数和差化积的方法计算，才可以确定两个同频率正弦量之和的模和初相角，即

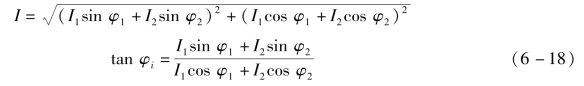
式（6－18）的求解过程也十分烦琐困难，从实用角度说，需要其他更简便的方法。

这里就介绍描述正弦量的第3种方法，即德国科学家施泰因梅茨提出的相量法。

1.正弦量的相量法

设有一个正弦量i＝Imsin（ωt＋φi），在复平面上作一个矢量，如图6－7所示。

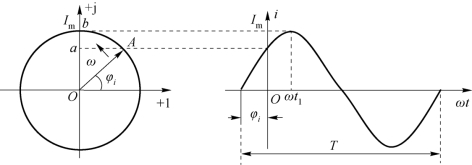
图6－7　正弦量的相量法

使矢量长度OA等于振幅值Im，矢量与横轴的夹角等于初相φi，矢量以ω的角速度绕坐标原点O沿逆时针方向旋转。在t＝0时刻，矢量在复平面虚轴上的投影是oa＝Imsinφi，对应了正弦量在t＝0时刻的瞬时值。经过t1时间后，矢量转到了与虚轴重合的位置，此时它在虚轴上的投影即ob＝Imsin（ωt1＋φi）就等于矢量自身的长度，也就是达到了最大值，该值也等于正弦量在t＝t1时刻的瞬时值。由此可见，这一旋转矢量每时每刻在虚轴上的投影都和正弦量的瞬时值对应，如此一来，该旋转矢量就能完整地表示一个正弦量。

复平面上的矢量可以用复数表示。我们用指数形式表示在起点位置时的这一矢量为，乘上旋转因子ejωt，可将任意时刻的矢量用复数表示出来，即

将该形式写成三角函数形式，即

该复数的虚部为正弦函数，对应了旋转矢量在虚轴上的投影。

由于在正弦交流电路中所有的激励和响应都是同频率的正弦量，使得旋转矢量的角速度ω一致，因此可以不考虑旋转，只考虑初始位置。也就是，在表示同频率的正弦量时，可以省去旋转因子ejωt，只用起始位置的复数来表示。

这种与正弦量相对应的复数就称为相量，用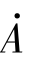表示，它是一个时间函数，但其本身并不等于正弦函数，而是能对应地表示一个正弦量。这就是正弦量的相量法。

一个正弦量i＝Imsin（ωt＋φi），它的相量可以写成

相量的模是正弦量的振幅，是振幅相量。如果写成有效值相量，则可以写成

一般未经特别说明的相量都指有效值相量。

如果将正弦量对应的复数画在复平面上，则这种表示相量的图就称为相量图。用相量表示的正弦量进行交流电路运算的方法就称为相量法。

例6－9　一并联电路中，两条支路上流过的电流分别为（ωt＋60°）A、（ωt－30°）A。写出两电流的相量，并画相量图。

解题步骤如下。

（1）从解析式可知两电流的有效值分别为

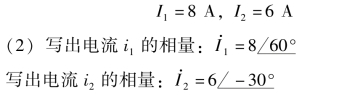
（3）画相量图。由相量的模和初相角确定两电流的位置，如图6－8所示。

图6－8　例6－9相量图

对极坐标形式的相量而言，还可以利用三角函数关系，分别求出相量的模在横轴与纵轴上的投影，从而将极坐标形式的相量改写成代数形式，

即

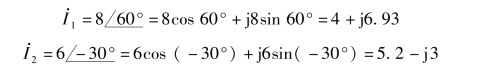
两相量的代数形式数值，可在图6－8中的实轴和虚轴上找到，它与极坐标形式是对应一致的。

例6－10　求例6－9中并联电路的总电流i。(www.xing528.com)

解题步骤如下。

方法一：

该结果与按平行四边形作图法得出的结果一致。

在实际情况下，两个同频率正弦量相加减，它们的振幅和相位差并不一定都满足勾股定理，因而后一种解法更为普遍，也更加简便。

将例6－10中后一种解法的解题过程与式（6－18）相比较，可以看出用相量的代数形式计算，再把计算结果转换成相量的极坐标形式，与采用三角函数和差化积法解出的式（6－18）的结果是完全一致的，但相量法明显简洁了很多。

通过上例也证明了正弦量和的相量等于正弦量的相量之和，即

同理，两个同频率正弦量之差也可以用相量法求解。求解时，可看作一个相量加上另一个取反后的负相量。取反后的负相量在相量图上与原相量方向相反。

2.基尔霍夫定律的相量形式

如前几章所述，基尔霍夫定律在交流电路中也同样适用。也就是说，在任意时刻，对任一电路节点而言，流过该节点的各电流瞬时值的代数和等于零，即∑i＝0；对任一闭合回路而言，回路内各段电压瞬时值的代数和等于零，即∑u＝0。

由于描述正弦量按时间规律变化的解析式，表达的也是交流电路中电流或电压瞬时值的变化，因此基尔霍夫定律也可以描述成：在任一时刻，任一节点上各支路电流的解析式的代数和等于零。同理，在任一时刻，任一回路内各段电压解析式的代数和等于零。

在正弦交流电路中各电流和各段电压都是与电源同频率的正弦量，同频率三角函数形式的运算如前所述，都可以用对应的相量运算来替代。因而将这些同频率的正弦量用相量表示，可得

式（6－22）表示，流过正弦交流电路中的任一节点电流的相量代数和等于零。电流的正负号由参考方向决定。这就是基尔霍夫电流定律（KCL）的相量形式。

同理，将同频率的电压正弦量用相量表示，可得

式（6－23）表示，正弦交流电路中，任一回路内各段电压的相量的代数和等于零。这就是基尔霍夫电压定律（KVL）的相量形式。

练一练：

已知在一串联回路中，电源u＝10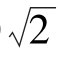sin（ωt＋36.9°）V施加在两个元件上。其中一个元件电压是u1＝5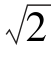sin（ωt－53.1°）V，求另一个元件上的电压u2，并画出相量图。

（1）根据KVL的相量形式，可写出

（2）写出电源电压u的相量并转换成a＋jb的形式：_______________。

（3）写出电压u1的相量并转换成a＋jb的形式：__________________。

（4）计算并画相量图。

（5）写出u2的解析式：______________________________________________________。

解题微课

知识点归纳

（1）正弦量的三要素：振幅值Im或Um、角频率ω、初相位φ。角频率与频率f及周期T的关系是：

（2）正弦量的有效值与振幅值之间的关系是：I＝0.707Im，U＝0.707Um。

（3）同频率的正弦量之间有超前、滞后、同相、正交、反相等相位关系。

（4）正弦量有函数解析式，如i＝Imsin（ωt＋φi），以及波形图和相量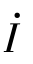或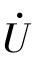三种表示法。

（5）正弦量的相量法一般可以写成极坐标形式或者代数形式。它们之间的转换关系是：和a＝Icosφ、b＝Isinφ。

（6）当同频率正弦量进行加减运算时，可以将相量写成代数形式，再将实部与实部相加减，虚部与虚部相加减；当正弦量进行乘除运算时，可以将相量写成极坐标形式，再进行模的相乘或相除，幅角的相加或相减。

（7）基尔霍夫电流定律和电压定律的相量形式分别是：