如何求解积分电路的阶跃响应曲线

1.阶跃函数

前几节所述的一阶电路，都是通过开关动作产生的动态响应。开关动作可以用阶跃函数来表示其数学模型。

单位阶跃函数是一种奇异函数，如图5－38（a）所示。函数在t＝0时发生了从“0”到“1”的阶跃，相当于开关发生了闭合动作。可定义为

若在t＝t0时刻发生了阶跃，如图5－38（b）所示，称为延迟单位阶跃函数，定义为

阶跃函数本身并没有量纲，它在表示电流时量纲为A，表示电压时量纲为V。利用阶跃函数可以方便地表示各种信号。比如：一个幅值为A的矩形脉冲信号就可以认为是由阶跃函数Aε（t）和－Aε（t－t0）叠加组成，如图5－39所示，其表达式为

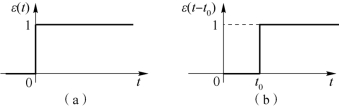
图5－38　阶跃函数

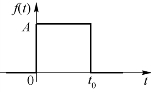
图5－39　矩形脉冲

2.阶跃响应

阶跃响应可以看作电路在阶跃函数的激励下产生的零状态响应。

在图5－40所示的电路中，电压源为一个幅度为A的阶跃函数。RC电路接通这一激励源后，电容C上的电压阶跃响应为

图5－40　RC阶跃响应

例5－12　已知电路如图5－41（a）所示，R1＝R2＝10kΩ，C＝100μF，uS为阶跃电压，其波形如图5－41（b）所示。试求uC、iC，并画出uC、iC的阶跃响应曲线。

解：方法一。

将uS信号分成0＜t＜0.5s和t＞0.5s两个时间段。在0＜t＜0.5s时间段视作电源接通，电路产生零状态响应；在t＞0.5s时间段视作电源断开，电路产生零输入响应。求解方法与前同，此处省略。

方法二。

uS可看作两个阶跃函数的叠加：uS（t）＝10ε（t）－10ε（t－0.5）。

为方便求解，将图5－41（a）先转化成图5－42所示的戴维南等效电路，则等效激励源和电阻是：

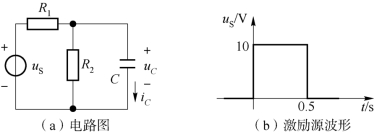
图5－41　例5－12电路图与激励源波形

图5－42　例5－12等效电路

时间常数为：

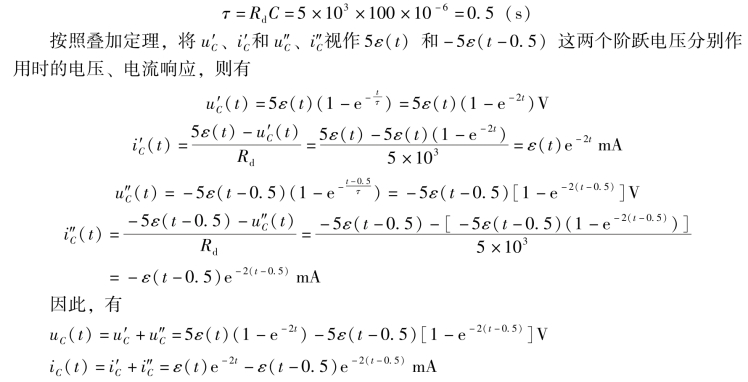
电压与电流的波形响应如图5－43（a）和图5－43（b）所示。

图5－43　例5－13题解波形响应

3.微分电路与积分电路(www.xing528.com)

当RC一阶电路受到一个方波脉冲激励时，则这个方波脉冲就相当于一个阶跃信号。若电路受到周期性的方波激励，则RC一阶电路将产生周期性的阶跃响应。

在这种周期响应中，当RC电路的输入输出信号构成微分关系时，此时的电路就称为微分电路；若输入输出构成的是积分关系，则称为积分电路。

1）微分电路

RC串联电路，如图5－44所示，取电阻端为输出端。

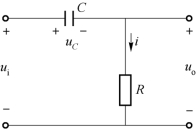
图5－44　微分电路

当输入电压ui是幅度为Ua、脉冲宽度为τa的周期性方波信号时，电路中的电容就被周期性地充、放电，充、放电的时间常数τ＝RC。

若满足τ≪τa，则电容充、放电能很快达到方波电压的幅度Ua或达到零值，这就使电容电压uC≈ui，则输出电压为

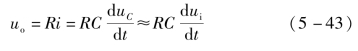
式（5－43）表明，满足条件τ≪τa时，电路的输入和输出电压构成微分关系，是微分电路。

此时电阻电压uR＝uo＝ui－uC，则在t＝0＋时刻，有

之后电阻电压随电容充电而下降。

在t＝τa＋时刻，电容已充满电，因而有

之后电阻电压随电容放电又逐步回到零值。因此，微分电路在电阻上的输出波形响应如图5－45所示，呈尖脉冲。

图5－45　微分电路输入输出波形

2）积分电路

RC串联电路如图5－46所示，取电容为输出端。输入周期性方波信号同上。电路的时间常数仍是τ＝RC。

若满足τ≫τa，则电容充电很慢，尚未充满时，输入信号变零，电容转入放电。同理，电容放电也慢，则未放电趋零时，输入信号跳变至Ua，电容又转为充电。如此往复，电容端的输出波形如图5－47所示。

若时间常数τ进一步减小，则电容上电压的充、放电波形将变得更小，此时电阻电压uR≈ui，则输出电压为

式（5－44）表明，满足条件τ≫τa时，电路的输入和输出电压构成积分关系，是积分电路。

积分电路的输出波形为锯齿波。

当积分电路与有源放大器件组合，则能放大锯齿波信号的幅度，呈现清晰的三角波形的形态，广泛应用于扫描电路中。

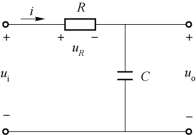
图5－46　积分电路

图5－47　积分电路输入输出波形

知识点归纳

（1）阶跃函数是开关动作的数学模型，单位阶跃函数用ε（t）或ε（t－t0）表示。

（2）阶跃响应可看作电路在阶跃函数的激励下产生的零状态响应。

（3）RC串联电路输入脉冲宽度为τa的方波信号，当满足τ≪τa时，电阻端输出尖脉冲，构成微分电路；在满足τ≫τa时，电容端输出锯齿波，构成积分电路。