用三要素法求解电容电压过渡曲线

1.三要素法的一般形式

通过前面的分析可知，一阶电路的全响应由稳态分量和暂态分量组成。稳态分量是电路换路后达到新的稳态的解，暂态分量则是从初始值向新的稳定值的过渡过程，其中的初始值由电路的初始条件确定，过渡过程的快慢则由时间常数τ决定。

因此，求解一阶电路的过渡响应，就存在着一种方法，只要知道电路换路后的稳态值、初始值和时间常数，就能直接写出一阶电路过渡过程的解，这就是三要素法。

设f（∞）是电压或电流的新的稳态值，f（0＋）是电压或电流的初始值，τ是电路的时间常数，则各类响应都可以用三要素法表示为

将前几节所述的各类响应用三要素法表示，可列出表5－6。

表5－6　各类响应的三要素表示法

从表5－6中可以看出，零输入响应和零状态响应是全响应的特例。

2.三要素法的求解步骤

应用三要素法求解一阶电路，不仅适用于较普遍的非零初始状态的全响应，也包含了零输入响应和零状态响应特例，使一阶电路的过渡过程分析更为简明。具体方法如下。

（1）确定初始值f（0＋）：利用在直流稳态情况下，电容C相当于开路，电感L相当于短路，求出在换路前t＝0－时的uC（0－）、iL（0－），并由换路定律得到uC（0＋）、iL（0＋）；再根据t＝0＋时换路后的电路，求解其他电压或电流的初始值f（0＋）。

（2）确定稳态值f（∞）：根据新直流稳态下的电路，求f（∞）。

（3）求时间常数τ：在RC电路中，τ＝RC；在RL电路中，τ＝L/R。其中R应理解为换路后将电路中所有独立电源置零后，从C或L两端看进去的等效电阻。

（4）由三要素公式写出电路中电压或电流的过渡响应表达式。

例5－10　已知电路如图5－35（a）所示，R1＝R2＝1kΩ，US＝10V，C＝10μF，电路已达稳态。t＝0时，S开关断开。试用三要素法求开关断开后的uC、iC，并画出uC过渡响应曲线。

解：（1）求解电压uC，有

图5－35　例5－10图

（2）求解电流iC有两种方法。

①求导法，即

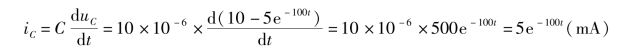(www.xing528.com)

②电路分析法，即

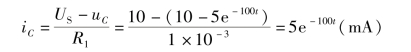
例5－11　已知电路如图5－36（a）所示，R1＝8Ω，R2＝5Ω，L＝4H，US1＝20V，US2＝10V，S处于中间位置，电路已达稳态。t＝0时，S合于位置1，t＝1s时，又将S合于位置2，试求iL，并画出电流的响应曲线。

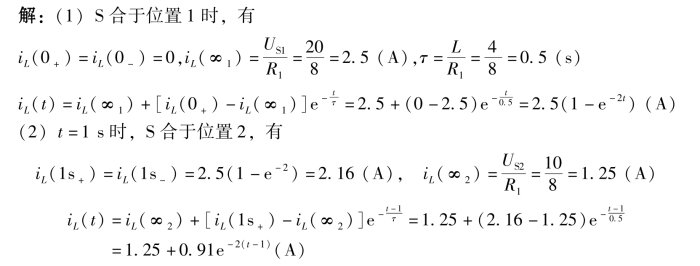
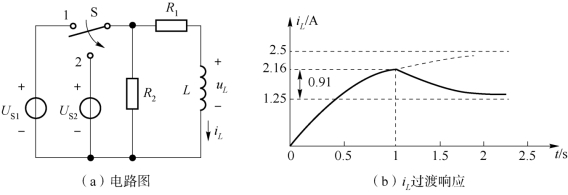
图5－36　例5－11用图

综上，电流iL过渡响应的波形如图5－36（b）所示。电感上电流总的响应则可以写成

练一练：

已知电路如图5－37所示，R1＝R3＝10Ω，R2＝5Ω，US＝20V，C＝10μF，电路已达稳态。在t＝0时刻，S开关闭合。试用三要素法求uC，并画出电容电压的过渡响应曲线。

需要关注的方法和步骤如下。

（1）根据S未闭合前电路及换路定律求得初始值uC（0＋）：________________________。

（2）根据新直流稳态下的电路求得稳态值uC（∞）：______________________________。

（3）求时间常数τ＝RC。其中R是换路后电路从电容C端看进去的戴维南等效电阻：____________________________________________________________________________。

（4）写出uC全响应表达式，并画出过渡响应曲线：_______________________________

图5－37　练一练题图

解题微课

知识点归纳

（1）一阶电路的全响应可以分解为暂态分量和稳态分量，也可以分解为零输入响应和零状态响应。

（2）一阶电路的三要素法：f（t）＝f（∞）＋[f（0＋）－f（∞）]。确定电路的稳态值、初始值和时间常数即可根据该式写出电路的过渡响应。

（3）RC电路的时间常数是τ＝RC，RL电路的时间常数τ＝L/R。R为换路后动态元件两端看进去的戴维南等效电阻。