RC电路的零状态响应分析

在图5－24所示电路中，开关S未合上前，如果电容上的电压为零，则电容处于零初始状态。在t＝0时，S闭合，电容C被电压源充电，电容上的电压就从零开始上升，最后上升到电源电压的值。

根据基尔霍夫定律，有

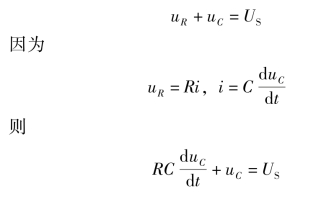
图5－24　RC零状态响应

该式为一阶常系数线性非齐次微分方程，它的解由特解和通解组成。由于电容充电充满这种状态，必然满足上式，因此可将它看作上式的一个特解，即uC′＝US。而该方程的通解为：

式（5－23）是电容在零状态接通电源以后，充电过程的电压uC的表达式。

接通激励电源后，电路中的电流为电容的充电电流，可用求导法求得，也可用电路分析法，求得电流，即

式（5－24）表明，在t＝0时刻电路接通瞬间，电流i为最大值US/R。随着电容充电，电阻R上的电压逐渐减小，充电电流逐渐衰减，直到趋于零。此时电容处在稳定状态，相当于开路。

根据式（5－24），又有电阻上电压为

零状态响应时，uC、uR和i随时间变化的曲线如图5－25所示。可以看出，充电时电容上的电压从零开始按指数规律上升直到趋向稳定值US，而电阻上的电压则从US按指数规律衰减直到趋近于零（图5－25（a））。充电电流也按同样规律衰减（图5－25（b））。电路的时间常数τ＝RC，R越大充电电流就越小，充电也就越慢；电容C容量越大，需要充电充满的时间也越长。表5－5给出了对应于不同时刻，uC电压达到的充电值。

表5－5　t为时间常数τ的整数倍时uC充电达到的电压值

图5－25　RC零状态响应时uC、uR和i随时间的变化曲线

例5－7　图5－26是一种测速装置的原理电路。已知电源US＝10V，电阻R＝10Ω，电容C＝100μF。A、B为金属导体，A、B相距s＝1m，当射击的子弹匀速地先击断A再击断B时，测得电压uC＝8V，求射击的子弹速度。

图5－26　例5－7电路图（应用电路：测速装置）

解题思路如下。

A、B金属在没有被击断时，电源US只与电阻R和金属A构成回路，电容相当于开路，电容上的电压为零。

因此uC（0－）＝0。

当金属A被击断时，电源US与电阻R、电容C和金属B构成回路，电容被充电。电容的初始值为

若充电充满，电容上的电压达到稳定值，即(www.xing528.com)

若电容未充满电，金属B就被击断，则电路断开。此时电压表显示的是电容已充电达到的值。

由此可知电路构成RC零状态响应。

解题步骤如下。

（1）电路充电的时间常数：τ＝RC＝10×100×10－6＝1（ms）

（2）电压uC的表达式：uC＝US（）＝10（1－e－1000t）V

（3）设金属B被击断的时间为t1，则根据题意有

解得：t1＝1.6ms。

（4）计算速度为

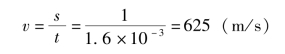
练一练：

在图5－24所示电路中，R＝10kΩ，C＝4μF，US＝250V，电容初始电压为零。求：（1）开关S合上后电容上电压和电流的零状态响应；（2）要经历多久电容电压可以充到180V？

解题微课

需要关注的方法和步骤如下。

（1）求出时间常数τ：_________________________________________。

（2）写出充电电压uC的表达式：________________________________。

（3）写出充电电流i的表达式：_________________________________。

（4）根据式，在τ、US和uC已知的条件下，求经过的时间t，要使用ln函数：________________________________________________________。

（5）对于，用lnx函数线求得t：________________________________________。

知识点归纳

（1）RC一阶电路零输入、零状态响应分别对应电容的放电、充电过程。

（2）利用电容电压不突变，可知零输入响应时电容电压的初始值。

（3）利用电容在稳定状态下相当于开路，可知零状态响应时电容电压的稳态值。

（4）时间常数τ＝RC，它由换路后充、放电回路中的元件参数决定，它决定了过渡过程的快慢。

（5）在求得电容电压过渡过程的基础上，可根据电路分析或微分求导解出电流等其他参数的过渡过程表达式。