电容和电感的串并联技巧

1.电容的并联

电容并联如图5－13所示。所有电容同处一个电压u，则各极板上的电荷量为此时，极板上总的电荷量q＝q1＋q2＋…＋qn。

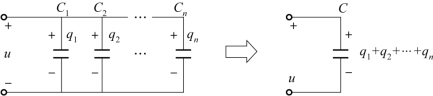
图5－13　电容的并联等效

例如，有一电容，能在同样的电压下存储电荷量q，则此电容C即为n个电容的等效电容。其等效关系为

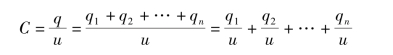
进一步可得

即几个电容并联时，等效电容等于各个电容之和。

2.电容的串联

电容串联如图5－14所示。由于仅有串联的首尾两块电容极板与电源相连，因此电源就使这两块极板带上等量的异种电荷，其他中间的极板则因静电感应才出现等量的异号电荷。因而每个电容上的电荷量均为q。电路的总电压u＝u1＋u2＋…＋un。

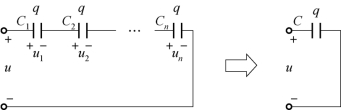
图5－14　电容的串联等效

此时，每个电容上的电压分别为

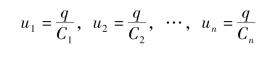
总电压可写为

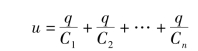
由于总电压与串联等效电容满足，因此有，可得

式（5－13）表明，电容串联时，等效电容的倒数等于各电容倒数之和。

由每个电容上的电压也可推出

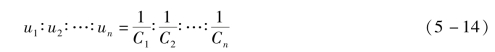
式（5－14）表明，电容串联时，各电容的电压与电容容量成反比，即电容小的承受较高的电压，电容大的反而承受较小的电压。

例5－3　已知3个电容器如图5－15所示连接，C1＝60μF，C2＝20μF，C3＝10μF，每个电容器的耐压均为50V。求：（1）等效电容；（2）电路端电压接上75V时是否超出电容的耐压？

解：（1）C2、C3并联后电容为

C23＝C2＋C3＝20＋10＝30(μF)

C1与C23串联，电容为

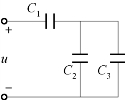
图5－15　例5－3电路图

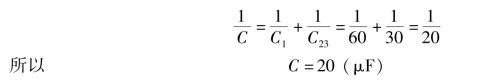(www.xing528.com)

（2）记C1上的电压为u1，C2和C3并联后C23两端的电压u23，则有

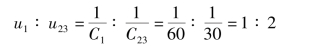
端电压为75V时，u1＝25V，u23＝50V。未超过电容耐压50V。

需要关注的方法和步骤如下。

（1）分别求串、并联等效电容。

（2）电容并联时，电压不允许超过并联电容中最低的耐压。

（3）电容串联时，电容较小的分得较大的电压。因此要首先满足小容量的电容不超过其耐压值。

练一练：

有两个电容器C1＝250μF、C2＝50μF，耐压分别为450V和250V。求：

（1）并联使用时的等效电容及允许的工作电压：_________________________________。

（2）串联使用时的等效电容及允许接入的端电压：_______________________________。

解题微课

3.电感的串并联

两个电感连入同一个电路，则不可避免地会发生其中一个电感线圈的磁链变化穿过另一个线圈，从而使另一个线圈产生感应电动势。这种现象称为互感。而一个线圈的磁链交链到另一个线圈则称为互耦。关于互感和互耦的详细分析将在后续章节论述。

在无互耦的理想情况下，或者在互耦影响可忽略不计的情况下，n个电感串联，如图5－16（a）所示，其等效电感L为各个电感的自感量之和，即

n个电感并联，如图5－16（b）所示，等效电感L的倒数等于各电感的倒数之和，即

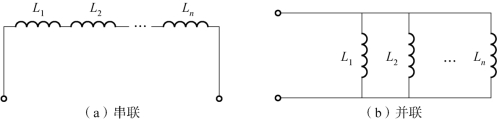
图5－16　电感的串、并联

知识点归纳

（1）电容器可以存储电荷。电容器存储电荷的能力称为电容量，也简称电容，其定义为电荷量q与电容器两端电压u的比值，用C表示，即。

（2）电容元件上电压与电流的关系为：。电容上的电流与电容上电压的变化率有关。电容上电压变化越快，流过的电流越大；反之流过的电流越小。当电容上电压无变化时，流过电流为零，相当于开路。

（3）电容元件的储能为：

（4）电容串联等效电容的倒数等于各电容倒数之和，即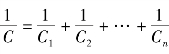；电容并联等效电容等于各个电容之和，即C＝C1＋C2＋…＋Cn。

（5）电感器可以存储磁场。电感器存储磁场的能力称为自感量或电感量，也简称电感，其定义为磁链Ψ与流过电感器的电流iL的比值，用L表示，即

（6）电感元件上电压与电流的关系为：。电感上的电压与电感电流的变化率有关。电感上电流变化越快，感应产生的电压越大；反之感应产生的电压越小。电感上电流无变化时，电感上的电压为零，相当于短路。

（7）电感元件的储能为：

（8）电感串联等效电感L为各个电感的自感量之和，即L＝L1＋L2＋…＋Ln；电感并联等效电感等于各个电感量的倒数之和，即