电路理论中的对偶定理及其应用

在对电路进行分析研究的过程中，可以看出某些电路元件、参数、结构、变量、定律和定理等都存在成对出现的一一对应关系。

图4－25是两个电阻的串联电路，图4－26所示为两个电导的并联电路。分别列出这两个电路的表达式，即

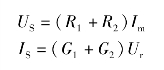
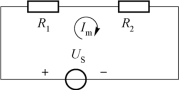
图4－25　两个电阻的串联电路

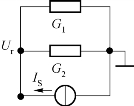
图4－26　两个电导的并联电路

根据上面两组关系式可以得到：若将对应的参数、变量和相应的电路结构进行互换，即R与G互换、U与I互换、串联与并联互换，则上述两组关系式可以彼此互换。即在两组关系式中，其数学表达式的形式完全相同，所不同的仅仅是式中的文字和符号，并且两组关系中的各元素都属于电路系统。这样两个通过对应元素互换能够彼此转换的关系式称为对偶关系式。关系式中能互换的对应元素称为对偶元素。符合对偶关系式的两个电路相互称为对偶电路。

由此可归纳出电路的对偶原理，其表述为：如果将一个网络N的关系式中_各元素用它的对偶元素对应地置换后，所得到的新关系式一定满足与该网络相对偶的网络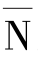。或者说，若两个电路对偶且对偶元件参数的数值相等，则两者对偶变量的关系式（方程）及对偶变量的值（响应）一定完全相同。

例4－11　网孔电路如图4－27所示，节点电路如图4－28所示，分别列出电路方程，并判断它们是否为对偶电路。

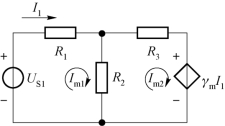
图4－27　例4－11网孔电路图

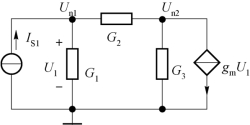
图4－28　例4－11节点电路图

（1）列出图4－27所示电路的网孔方程，即(www.xing528.com)

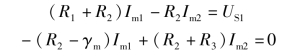
（2）列出图4－28所示电路的节点方程，即

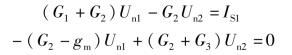
按照上面的分析过程，可以看出这两个电路的元件和电路的结构特点：将网孔各元素变成与其对偶的相应元素后，即得节点方程。因此，两电路为对偶电路。

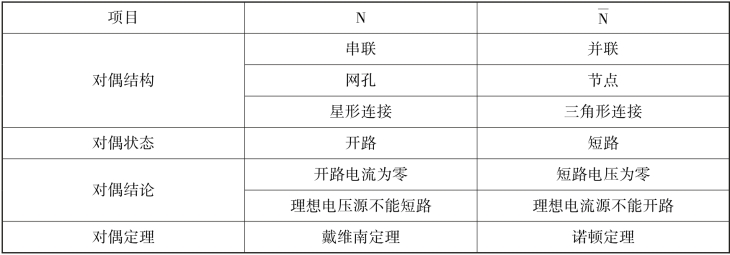
从上述分析过程可以总结出电路中的对偶关系如表4－2所示。

表4－2　电路总的对偶关系

续表

知识点归纳

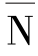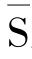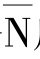对偶定理的概念为：两个对偶电路N、，如果对电路N有命题（或陈述）S成立，则将S中所有元素分别以其对应的对偶元素替换，所得命题（或陈述）对电路成立。

对偶原理的内容十分丰富。其应用价值在于，若已知原网络的电路方程及其解答，则可根据对偶关系直接写出其对偶网络的电路方程及其解答，收到了事半功倍的效果。此外，电路理论中的许多原理和结论，可以利用对偶原理予以分析、证明和掌握。

课后思考

（1）请列出大家学过的电路中的各种对偶关系。

（2）试用对偶定理证明诺顿定理。