基于流水线结构的算法优化措施

将图4-7圆周CORDIC迭代算法展开，并在每一级加入寄存器，就可以得到并行流水线结构的CORDIC算法。圆周CORDIC算法的流水线结构如图4-8所示，由图4-8可以看出，流水线结构的CORDIC算法具有以下特点：

（1）经过固有的等待时间后，每个时钟周期可以输出一个指定旋转操作的结果。

（2）移位操作的次数固定，因此可以用简单的重新联机（Rewiring）实现。

（3）常数角度值直接用硬件表示，无需查找表。

由于大多数FPGA在每个逻辑单元后都有一个寄存器，所以使用流水线结构不会增加硬件成本。

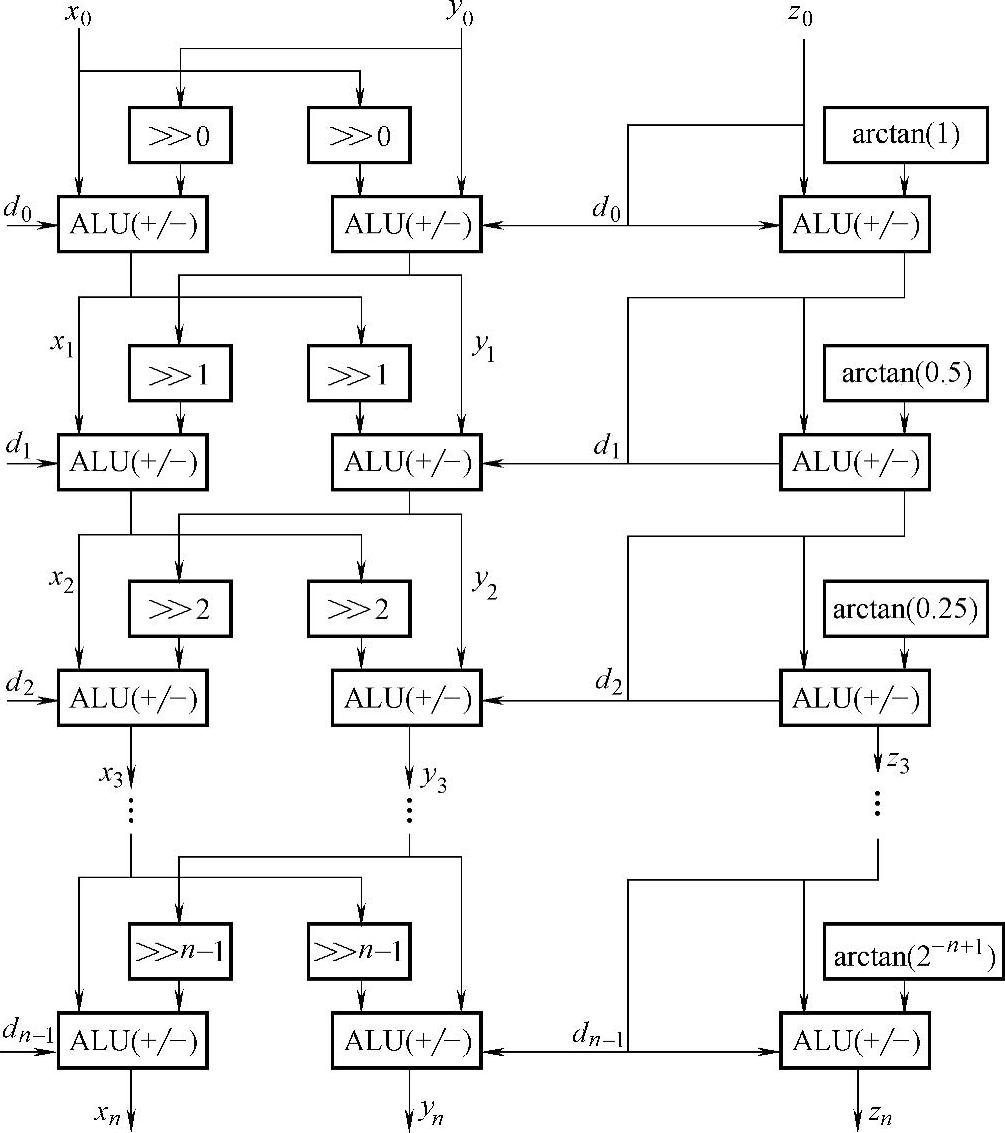
图4-8 圆周CORDIC流水线结构框图

对于圆周旋转模式的CORDIC算法，若令y₀=0，x₀=1，z₀=f（输入的角度值），则经过CORDIC旋转操作的结果为

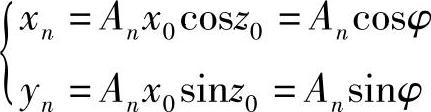
即最后一级的x分量与y分量的值分别对应于放大A_n倍的正弦值、余弦值。如果进一步令x₀=1/A_n，则(www.xing528.com)

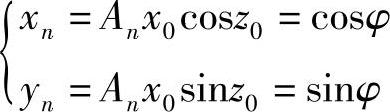
最终可以得到实际的没有放大的正弦值、余弦值。

由于在CORDIC算法中，输入的角度值、输出的正弦值、余弦值及其中间值都为小数，并且有正、有负，因此必须考虑数的表示方法。CORDIC算法中几乎不含乘法运算（仅有移位元加），所以用二进制定点数表示比较方便。任意实数X的二进制定点数表示为

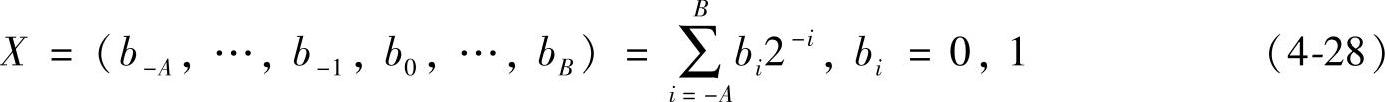
式中，A为整数数字的个数；B为小数数位的个数。

例如，十进制数（5.25）10可以表示为

（5.25）₁₀=（101.01）₂=1×2²＋0×2¹＋1×2⁰＋0×2^-1＋1×2-2

输入的角度值及z分量均采用弧度值，范围为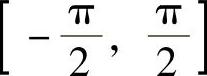，比角度值使用更少的字长。输出的正弦值、余弦值及相应的x和y分量的范围为（-1，1），角度值、输出的正弦值、余弦值及其中间结果均采用二进制补码格式的定点数。

关于CORDIC算法的字长与精度的问题，为了简化，作如下假设：旋转角度的近似值由最后一级的基本旋转角决定，对于n次迭代，该角度为arctan（2^-（n-1））；输入操作数的小数部分长度为n-1，则机器内部字长W=3＋（n-1）＋log₂（n），其中包括了保护位和溢出位；比例因子的小数部分长度为（n-1）＋log₂（n）。采用上面的数据长度时，近似误差小于2^-（n-1）。