CORDIC理论算法与优化探讨

CORDIC的相关算法包括旋转（rotation）模式和向量化（vectoring）模式。假设在笛卡儿坐标下有向量（x，y），按图4-1所示的方向旋转角度φ得到向量（x₁，y₁），则二者的关系为

式（4-1）可进一步写为

式（4-2）中，设tanφ=±2^-i，则tanφ与x或y的乘积相当于对当前坐标进行移位。由此可知，假设要旋转任意角度θ，则整个过程如图4-2所示，先经过旋转多个预设的角度α_i，最后才到达θ角位置，其表达式为

式中，d_i表示旋转方向；α_i表示旋转大小值；n表示旋转次数。

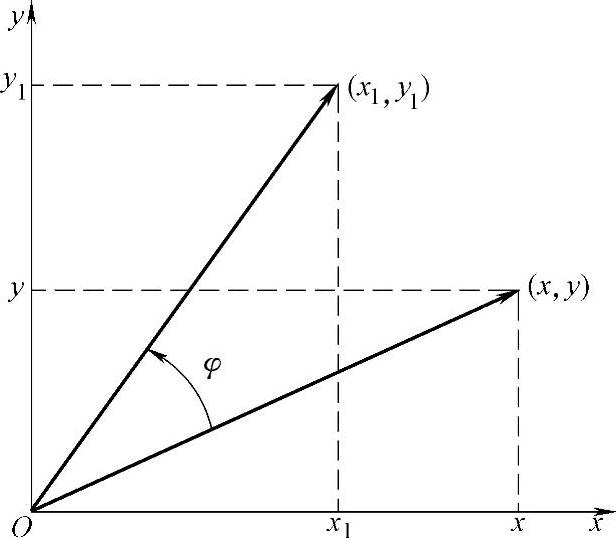
图4-1 笛卡儿坐标下向量的旋转

图4-2 使用连续的预定角度对向量旋转

由于每次旋转的角度为预定义的值，所以cosα_i也为常数，因此旋转任意角度θ的每次迭代处理可写成

式中，。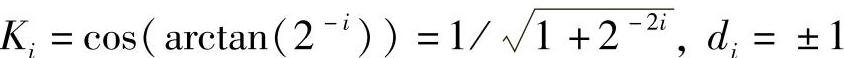

如果将比例常数K_i从迭代方程中去掉，则式（4-4）的方程就仅有移位加（shift-add）运算。K_i的乘积可以在整个系统的任何部分处理（不一定在CORDIC中完成），或者可以直接作为系统处理的增益。在式（4-4）中，当i趋近无穷的时候，K_i取得极限0.6037。所以，整个系统的增益A_n近似为1.647。当然，A_n实际值为

下面引入一个辅助变量z_i，为每次旋转预定角度的累加值，并且用来决定下次旋转的方向。则有

z_i＋1=z_i-d_i·arctan（2^-i） （4-6）

式中，d_i表示旋转方向。

CORDIC算法有旋转模式和向量化模式。在旋转模式中对向量指定旋转的角度，角度累加器初始值为需要旋转的角度值。在整个迭代过程中，旋转的方向用于减小角度累加器中剩余的角度值。所以，旋转方向由每一步迭代后的剩余角度的符号确定。CORDIC算法旋转模式的差分方程为

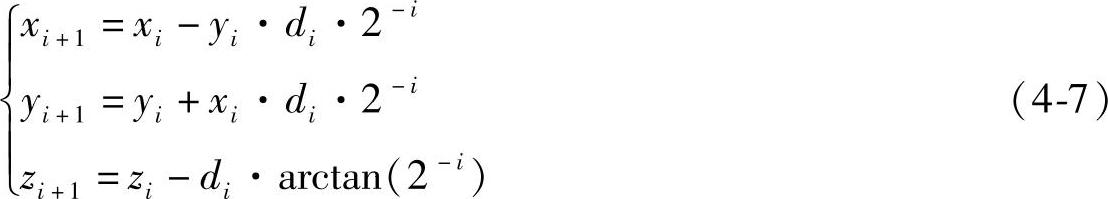(www.xing528.com)

式中

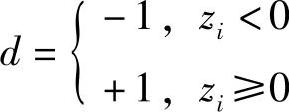
因此，旋转模式的最终结果为

在向量化模式中，CORDIC将输入的任意向量通过旋转一系列的预定角度，最终使向量与x轴对齐。向量化模式的结果为所有旋转的角度的累加值以及输入向量定标后的幅度值（结果在x分量中），分量y的符号用于决定下一次的旋转方向。角度累加器初始值为0，整个迭代结束后，其值为最终旋转的角度值。向量化模式的差分方程为

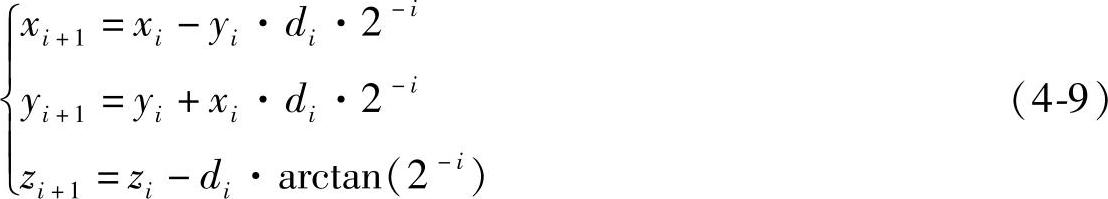
式中

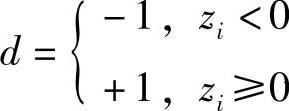
因此，向量化模式的最终结果为

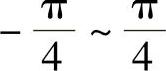在上面描述的CORDIC算法中，不管旋转模式还是向量化模式，第一次迭代时用的正切值为，所以整个旋转的角度都限定为。如果令初始旋转的角度为±π/2，则CORDIC算法可以实现大于π/2的旋转角度，则有

式中

此外，也可用下式的初始旋转公式替代式（4-11），即

式中

式（4-12）的初始旋转角为π或者0，同样可以实现大于π/2的旋转角度。

上面描述的CORDIC算法可以用来直接或者间接的计算三角函数值、反三角函数值、向量的幅值以及笛卡儿坐标和极坐标的变换等，下面分别介绍。