1.低矩形件拉深工艺计算
这里指的低矩形件包括一次拉深成形的Ⅱa、Ⅱb和较高深度的Ⅱc区,以及需两次拉深,但第二次近似整形的Ⅰa区。
1)按上述公式和方法计算确定毛坯尺寸。
2)计算相对高度H/B与表5-23所列的H1/B1相比,若H/B<H1/B1,则可一次拉深成形,若H/B>H1/B1,则不能一次拉深成形。
3)核算角部的拉深系数。对于低矩形件,由于圆角部分对直边部分的影响相对较小,圆角处的变形最大,故变形程度用圆角处的拉深系数表示

式中 r1——角部圆角半径(mm);
Ry——毛坯圆角部分的假想半径(mm),见图5-15,Ry=R。
若m1大于表5-24中的m1时,则可一次拉深成形,若小于表5-24中的m1,则不能一次拉深成形。
当r1=rd时,一次拉深变形也可用矩形件的比值H/r来表示

矩形件角部第一次拉深系数m1见表5-24。矩形件一次拉深许可的最大比值H1/r1见表5-25。
表5-23 一次所能拉深成形矩形件的最大相对高度H1/B1
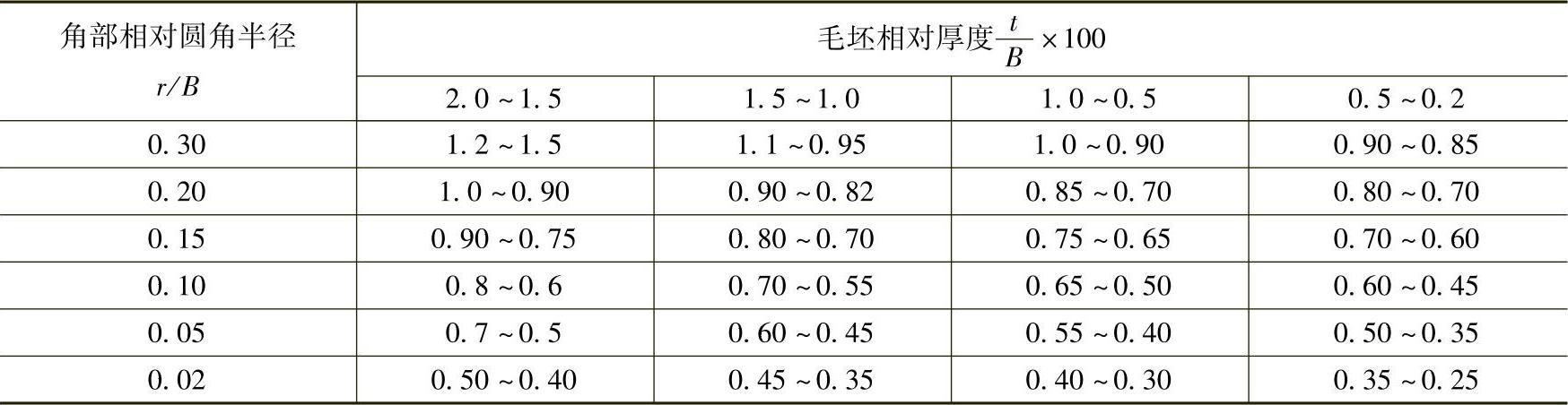
注:1.表中所列数据适用于08钢和10钢,对于其他材料,应根据金属的塑性加以修正,例如20~25钢带修正系数为0.85~0.9。 2.对于较小尺寸的矩形件(B<100mm)取较大值,对大尺寸的矩形件取较小值。
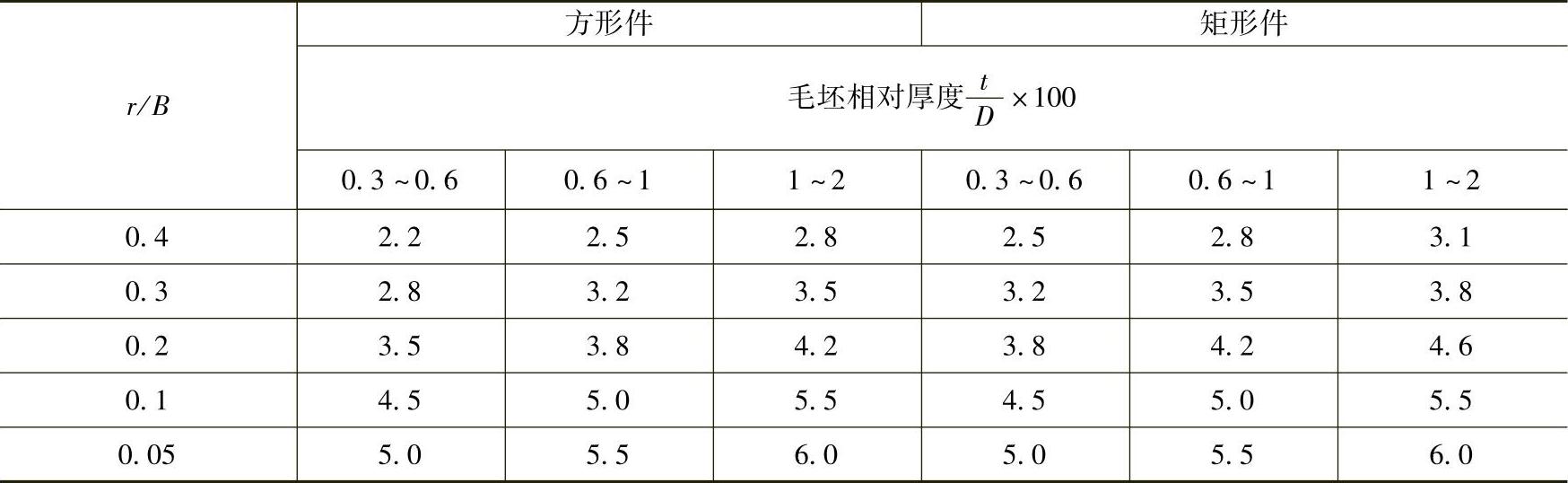
表5-24 矩形件角部第一次拉深系数m1

注:1.表中所列数值适用于08钢,对于塑性差的材料,应适当加大,对于塑性好的材料,可适当减小。 2.D对于正方形指毛坯直径,对于矩形指坯料宽度。
表5-25 矩形件一次拉深许可的最大比值H1/r1
2.高正方形多次拉深工艺计算
(1)高正方形多次拉深工艺计算程序
1)初步估计拉深次数,根据制件相对厚度t/B和相对高度H/B,查表5-26初步估计拉深次数。
2)确定毛坯形状和尺寸,根据制件相对高度H0/r查表5-21确定修边余量,再根据公式(5-18)或(5-19)计算毛坯直径。
3)校核是否需要多次拉深成形,根据r/B、(t/D)×100查表5-25校核是否需要多次拉深成形。
4)确定各次拉深工序件尺寸,根据r/B查表5-27求角部壁间距δ或当(t/D)×100=2或B=50t时查图5-19求直边壁间距bn,确定各次拉深工序件尺寸。
(2)采用角部壁间距δ的方法确定各次拉深工序件尺寸 图5-20a所示为方形件多工序拉深工序件形状和尺寸。采用直径为D的毛坯,各中间工序都拉成圆筒形,最后一道拉成方形件。
计算从n-1道工序开始,n-1道工序件的直径为
dn-1=1.41B-0.82r+2δ (5-25)
式中 dn-1——n-1次拉深所得工序件内径(mm);
B——方形件边长(内形尺寸)(mm);
r——方形件角部内圆角半径(mm);
δ——角部壁间距(mm),δ值列于表5-27。
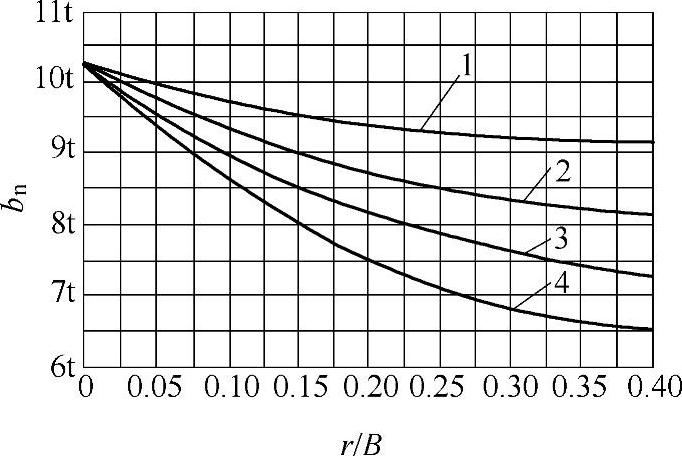
图5-19 bn数值与比值r/B及预拉深次数(1~4)的关系
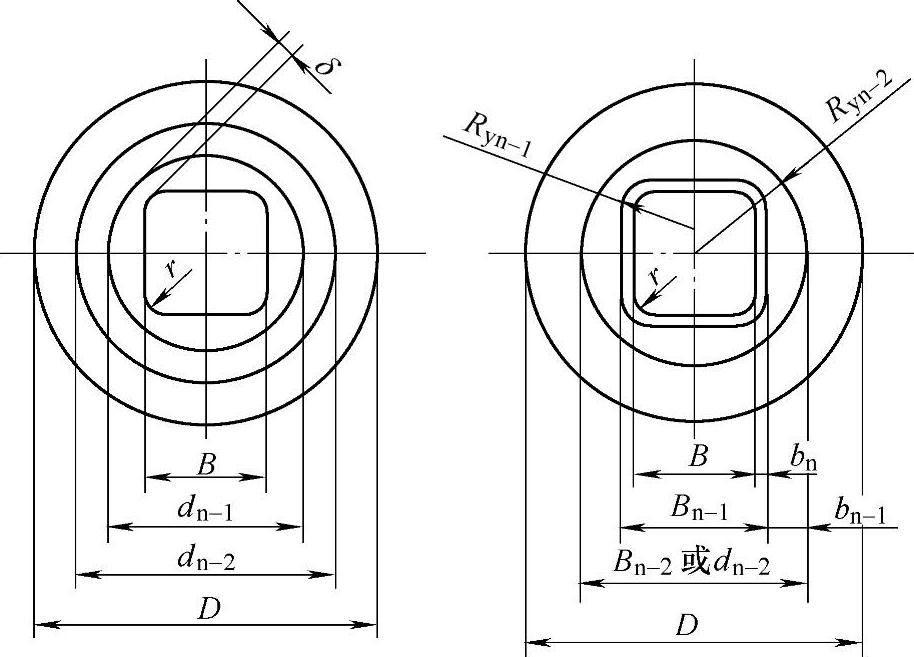
图5-20 高方形件拉深工序件形状和尺寸
表5-26 矩形件多次拉深所得能达到的最大相对高度H/B
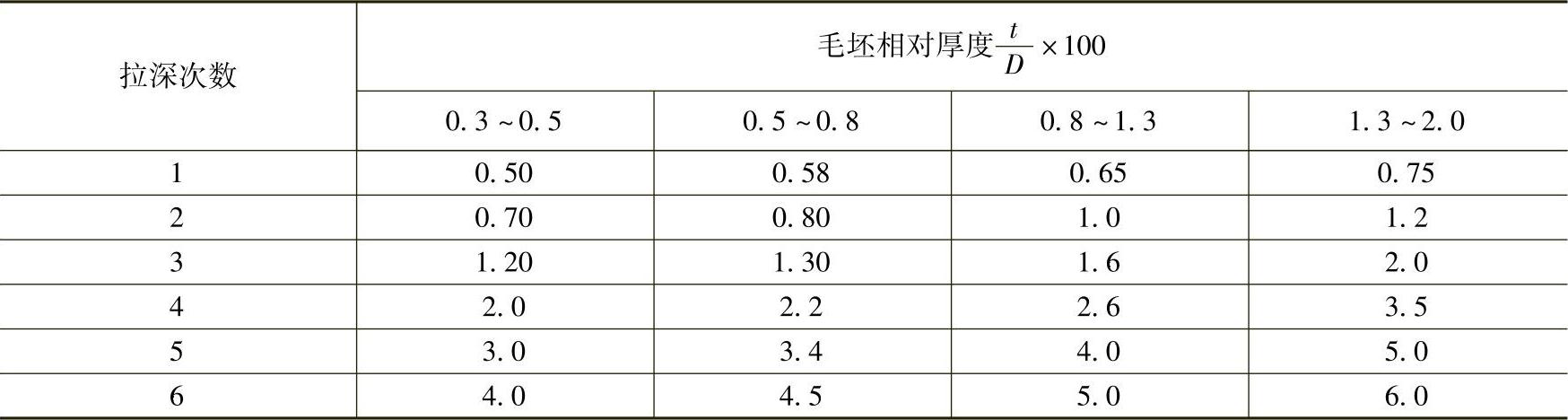
表5-27 角部壁间距δ值

表5-28 矩形件以后各次拉深系数
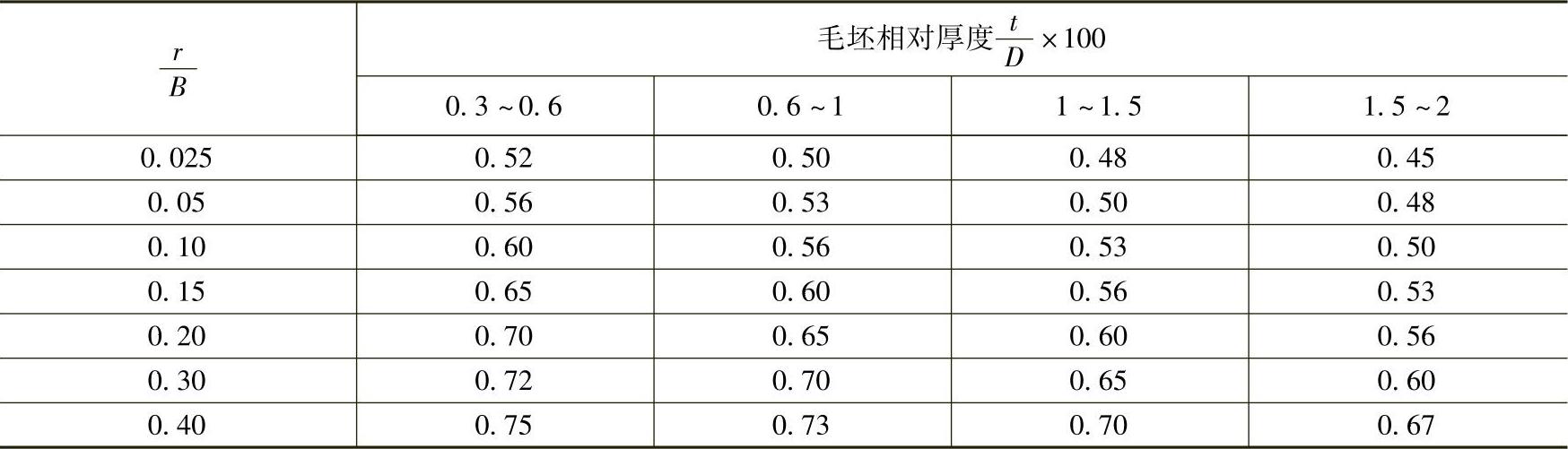
其他各道拉深工序相当于将直径为D的毛坯,拉深成直径为dn-1、高度为Hn-1的圆筒形件,因而工序件尺寸计算与圆筒形件拉深的计算方法相同。
采用角部壁间距实质上是选择适当的角部拉深系数作为工序件的计算基础,它适用于(t/B)×100≥2的拉深件。
(3)采用直边壁间距bn的方法确定各次拉深工序件尺寸 图5-20b所示为采用适当的直边壁间距bn的计算方法,这种方法实质上是以平均拉深系数作为工序件的计算基础。壁间距bn值可查图5-19。
采用直边壁间距bn方法是n-1道工序拉成较大圆角的方形件,最后再拉成方形件,其余工序拉深成圆筒形件。
计算从n-1道工序开始
By≈50t (5-26)
bn≤10t 查图5-19 (5-27)
Ryn-1=0.5By+bn (5-28)
Bn-1=B+2bn (5-29)
Hn-1=0.88H (5-30)
n-2道工序计算
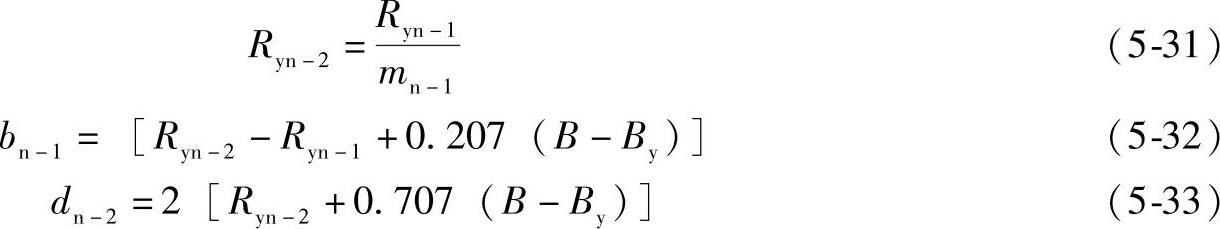
其他各道拉深工序相当于将直径为D的毛坯,拉深成dn-2,高度为Hn-2的圆筒形件,因而工序件尺寸的计算与圆筒形件拉深的计算方法相同。
例5-5 确定图5-21所示方形件拉深工序件的形状和尺寸。材料为08F钢,厚度为1mm。
1)初步估计拉深次数,根据制件相对高度H/B=70/44=1.59,相对厚度(t/B)×100=2.27,查表5-26。初步估计需三次拉深成形。
2)确定毛坯的形状和尺寸,根据制件的相对高度H0/r=70/3=23.3,查表5-21,修边余量ΔH=(0.05~0.08)H0=4mm,所以制件总高度为74mm。毛坯直径

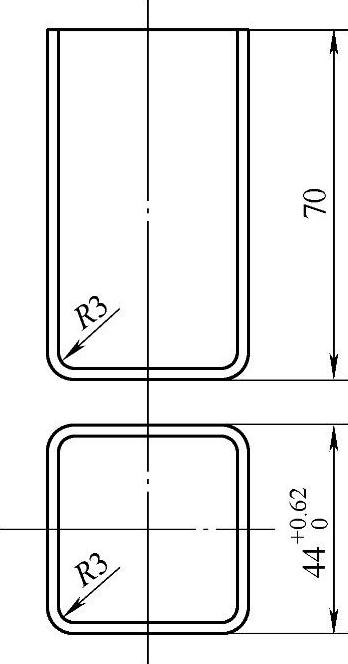
图5-21 方形制件图
3)校核是否需要多次拉深成形,根据r/B=3/44=0.068,(t/D)×100=(1/135.3)×100=0.74,查表5-25得矩形件第一次拉深许可的最大比值H1/r1≈5.3,故一次拉深的极限高度H1=5.3×3mm=15.9mm,所以不能一次拉深成形。
4)确定各次拉深工序件尺寸
① 计算从n-1道开始
根据r/B=0.068,查表5-27得
δ=0.132r=0.132×3mm=0.4mm
dn-1=1.41B-0.82r+2δ=1.41×44mm-0.82×3mm+2×0.4mm=60.4mm(https://www.xing528.com)
取rdn-1=4mm,则

② n-2道工序件尺寸计算。初步订拉深次数为3次,所以从n-2到n-1道的拉深属于第二次拉深,根据(t/D)×100=0.74,查表5-11取
m2(mn-1)=0.76,m1(mn-2)=0.56
得
而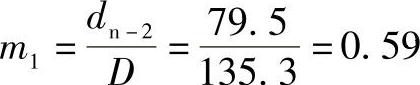 调整拉深系数:mn-1=m2=0.78
调整拉深系数:mn-1=m2=0.78
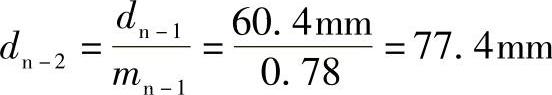
而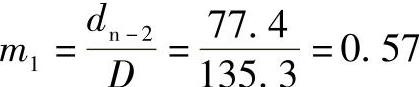
故从毛坯D=135.3mm,拉深到dn-2=77.4mm是可行的。
取rdn-2=6mm,则
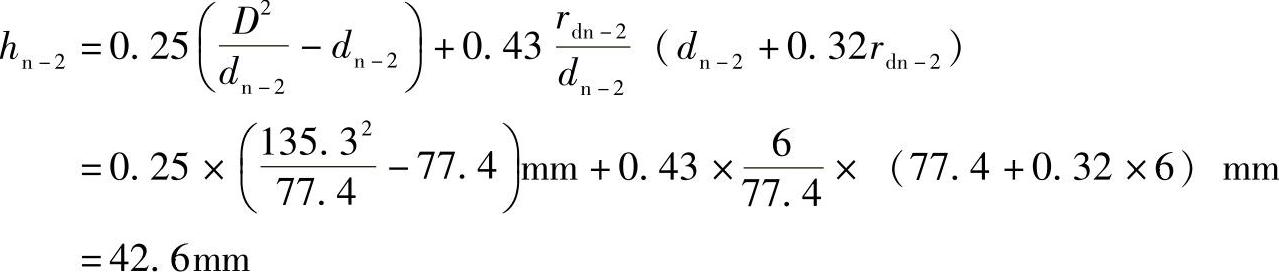
故制件三次拉深成形,各道工序件尺寸如图5-22所示。
例5-6 确定图5-23所示方形件拉深工序件的形状和尺寸。材料为08F钢,厚度为0.5mm。
(1)初步估计拉深次数 根据制件相对高度H/B=75/60=1.25,相对厚度(t/B)×100=(0.5/60)×100=0.83,查表5-26,初步估计需三次拉深成形。
(2)确定毛坯的形状和尺寸 根据制件相对高度H0/r=75/6=12.5,查表5-21,得ΔH=(0.04~0.06)H0=4mm,所以制件总高度为79mm。
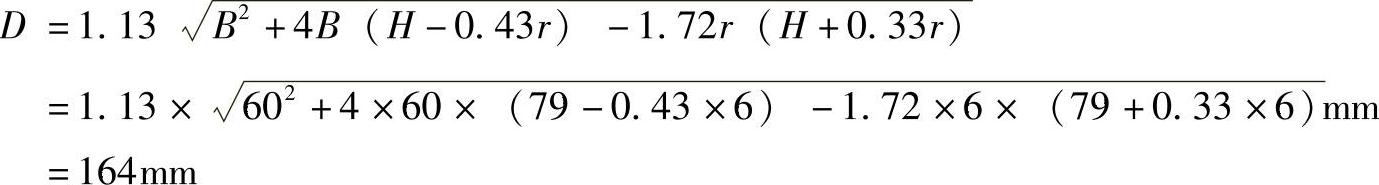
(3)校核是否需要多次拉深成形 根据r/B=6/60=0.1,(t/D)×100=(0.5/164)×100=0.3,查表5-25得矩形件第一次拉深许可的最大比值H1/r1≈4.5,故一次拉深的极限高度H1=4.5r1=4.5×6mm=27mm,而制件总高度为79mm,所以不能一次拉深成形。
(4)确定各次拉深工序件形状和尺寸
计算从n-1道工序开始
By=50t=50×0.5mm=25mm

图5-22 方形件拉深工序图
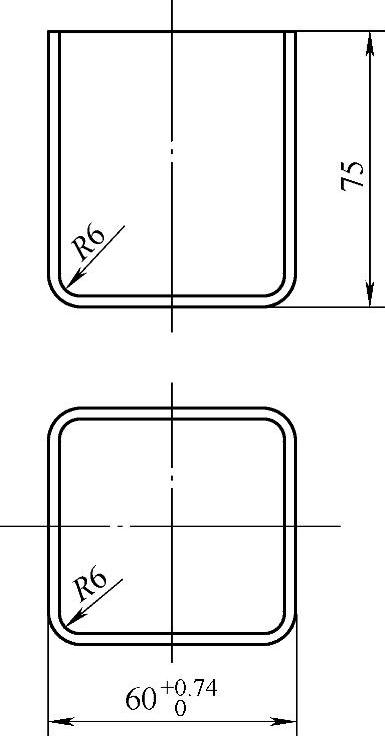
图5-23 方形制件图
根据r/B=0.1查图5-19和公式(5-26)~公式(5-32)得
bn=9t=9×0.5mm=4.5mm
Ryn-1=0.5By+bn=0.5×25mm+4.5mm=17mm
Bn-1=B+2bn=60+2×4.5mm=69mm
Hn-1=0.88H=69.5mm
初定拉深次数为三次,所以n-2道~n-1道的拉深属于第二道拉深,根据(t/D)×100=0.3,查表5-11得

取rdn-2=12mm

检查能否由毛坯D直接拉成dn-2,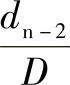
 ,在m1=0.56~0.58之间,故三次可拉深成形,各道拉深工序件尺寸如图5-24所示。
,在m1=0.56~0.58之间,故三次可拉深成形,各道拉深工序件尺寸如图5-24所示。
3.高矩形多次拉深工艺计算
图5-25所示是两种不同矩形件的拉深方法。第一种拉深方法的毛坯和中间工序是椭圆形,由半径分别为Ra和Rb的四个圆弧相接而成,而最后一道工序拉深成矩形,这种方法最后一次拉深材料变形不均匀性较大,容易局部起皱或破裂。因而适用于毛坯相对厚度较大,即(t/B)×100≥2,壁间距较小,即bn≤10t的矩形件。
第二种拉深方法的毛坯和中间工序过渡形状是长圆形,这种拉深方法的优点是给最后一次拉深创造了有利条件。拉深方法和工序件尺寸计算与方形件一样,都是从n-1道开始,计算程序及公式见表5-29。
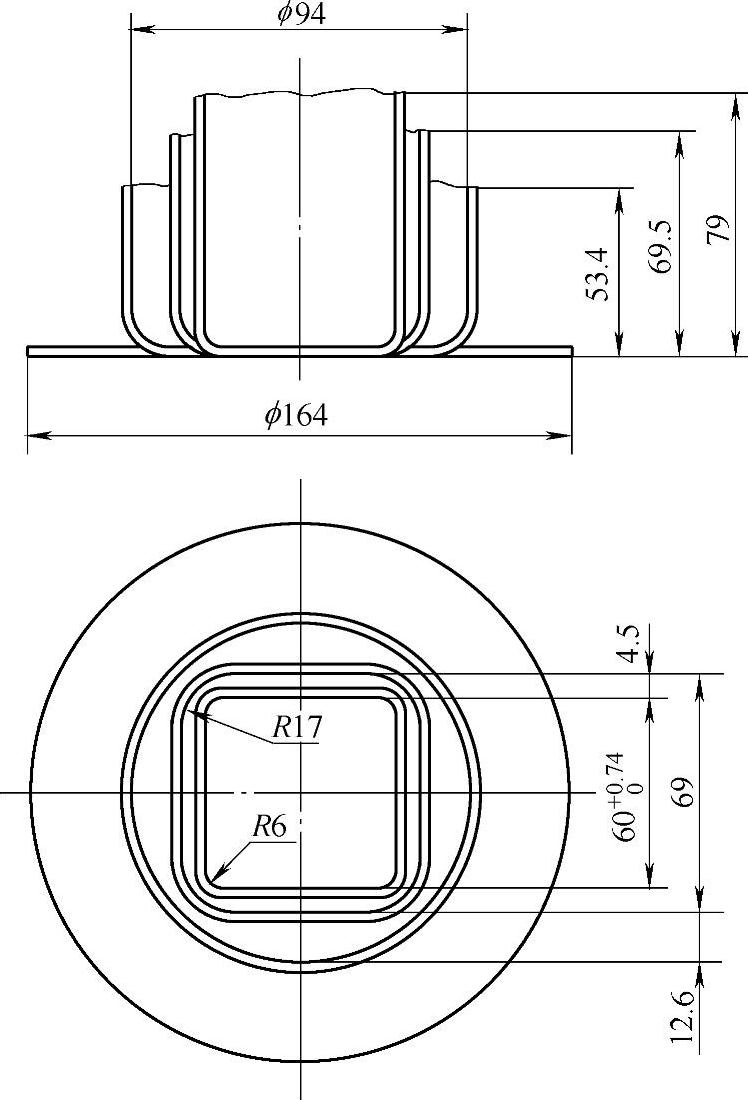
图5-24 方形件拉深工序图

图5-25 高矩形件多次拉深各道工序件的形状和尺寸
表5-29 高矩形件多次拉深的计算程序与公式

(续)

例5-7 确定图5-26所示的高矩形件工序件的尺寸和形状。材料为08F钢,厚度为1mm。
(1)检查相对厚度 圆角半径和相对高度分别为
(t/B)×100=(1/45)×100=2.22>2
R=8mm>6t
H=1.08H0=1.08×35mm=37.8mm,取38mm
H/B=38/45=0.84
查表5-26,可知该制件大约需两次拉深成形,可采用第一种方法。
(2)计算毛坯直径D
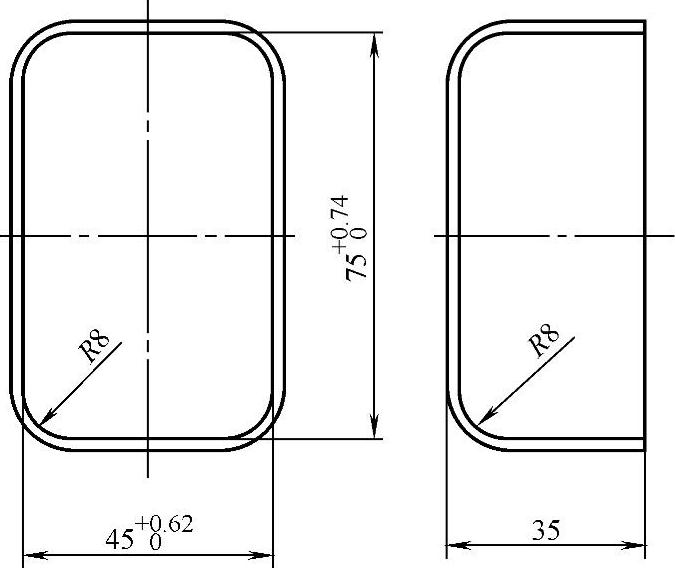
图5-26 高矩形件


(3)计算n-1次工序件尺寸


(4)检查Rb与Rbn-1的关系 因初步估计需两次拉深成形,所以Rbn-1=Rb1
(t/D)×100=(1/106.7)×100=0.94,r/B=8/45=0.18
查表5-24 m1=0.36
m=Rbn-1/Rb=Rb1/Rb=31.3/49.5=0.63>0.36
所以该制件两次拉深成形是可行的,工序如图5-27所示。

图5-27 高矩形件拉深工序图
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




